
题目列表(包括答案和解析)
 A.选修4-1:几何证明选讲
A.选修4-1:几何证明选讲
|
|
| α |
| α |
| β |
|
|
(本小题满分12分)
已知平面向量a=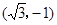 ,b=
,b=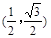
(1)证明a b;
b;
(2)若存在实数k,t,使x=a+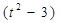 b,y=-ka+tb,且x
b,y=-ka+tb,且x y,试求k,t的函数关系式
y,试求k,t的函数关系式 ;
;
(3)根据(2)的结论,讨论关于t的方程 的解的情况。
的解的情况。
(本题满分12分)
设函数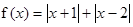
(1)将f(x)写成分段函数,在给定坐标系中作出函数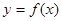 的图像;
的图像;
(2)解不等式f(x)>5,并求出函数y= f(x)的最小值。
(本小题满分12分)已知函数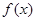 的定义域为(0,+∞),且满足对任意的
的定义域为(0,+∞),且满足对任意的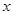 >0,y>0,
>0,y>0,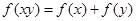 ,
,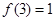 .当
.当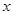 >1时,
>1时,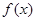 >0.
>0.
(1)求 的值
的值
(2)判断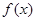 的单调性,并加以证明
的单调性,并加以证明
(3)解不等式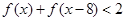 .
.
(12分)(1)作出y=|x+2|+|x+1|的图象;
(2)若关于x的不等式|x+2|+|x+1|<m的解集为 ,求m的取值范围.
,求m的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com