已知，函数

（1）当时，求函数在点(1，)的切线方程；

(2)求函数在[－1，1]的极值；

(3)若在上至少存在一个实数x₀，使>g(x_o)成立，求正实数的取值范围。

【解析】本试题中导数在研究函数中的运用。（1）中，那么当时，  又    所以函数在点(1，)的切线方程为；（2）中令   有 

对a分类讨论，和得到极值。（3）中，设，，依题意，只需那么可以解得。

解：（Ⅰ）∵  ∴

∴  当时，  又    

∴  函数在点(1，)的切线方程为 --------4分

（Ⅱ）令   有 

①         当即时

	（－1，0）	0	（0，）		（，1）
	+	0	－	0	+
		极大值		极小值

故的极大值是，极小值是

②         当即时，在（－1,0）上递增，在（0,1）上递减，则的极大值为，无极小值。 

综上所述   时，极大值为，无极小值

时  极大值是，极小值是        ----------8分

（Ⅲ）设，

对求导，得

∵，    

∴ 在区间上为增函数，则

依题意，只需，即 

解得  或（舍去）

则正实数的取值范围是（，）

 

已知函数f(x)=6x–6x²，设函数g₁(x)=f(x), g₂(x)=f［g₁(x)］, g₃(x)=f ［g₂(x)］,…g_n(x)=f［g_n–1(x)］,…

（1）求证:如果存在一个实数x₀，满足g₁(x₀)=x₀，那么对一切n∈N，g_n(x₀)=x₀都成立；

（2）若实数x₀满足g_n(x₀)=x₀，则称x₀为稳定不动点，试求出所有这些稳定不动点；

（3）设区间A=（–∞,0）,对于任意x∈A，有g₁(x)=f(x)=a＜0, g₂(x)=f［g₁(x)］=f(0)＜0，

且n≥2时，g_n(x)＜0  试问是否存在区间B（A∩B≠），对于区间内任意实数x，只要n≥2，都有g_n(x)＜0.

有以下五个命题
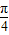①设a＞0，f（x）=ax²+bx+c，曲线y=f（x）在点P（x，f（x））处切线的倾斜角的取值范围为[0，]，则点P到曲线y=f（x）对称轴距离的取值范围为[0，]；
②一质点沿直线运动，如果由始点起经过t称后的位移为，那么速度为零的时刻只有1秒末；
③若函数f（x）=log_a（x³-ax）（a＞0，且a≠1）在区间内单调递增，则a的取值范围是；
④定义在R上的偶函数f（x），满足f（x+1）=-f（x），则f（x）的图象关于x=1对称；
⑤函数y=f（x-2）和y=f（2-x）的图象关于直线x=2对称．其中正确的有    ．

有以下五个命题
①设a＞0，f（x）=ax²+bx+c，曲线y=f（x）在点P（x₀，f（x₀））处切线的倾斜角的取值范围为[0，

π

4

]，则点P到曲线y=f（x）对称轴距离的取值范围为[0，

1

2a

]；
②一质点沿直线运动，如果由始点起经过t称后的位移为s=

1

3

t3-

3

2

t2+2t，那么速度为零的时刻只有1秒末；
③若函数f（x）=log_a（x³-ax）（a＞0，且a≠1）在区间(-

1

2

，0)内单调递增，则a的取值范围是[

3

4

，1)；
④定义在R上的偶函数f（x），满足f（x+1）=-f（x），则f（x）的图象关于x=1对称；
⑤函数y=f（x-2）和y=f（2-x）的图象关于直线x=2对称．其中正确的有．