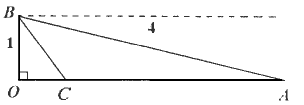
如下图，一条河宽1千米，相距4千米(直线距离)的两座城市A和B，分别位于河的两岸(城市A，B与岸的距离忽略不计)．现需铺设一条电缆连通城市A与B．已知水下电缆的修建费为4万元/千米，地下电缆的修建费为2万元/千米，假设两岸是平行直线，问：应如何铺设电缆可使总费用最少？(＝3.873，＝1.732，精确到百米，百元)

如下图，一条河宽1km，相距4km(直线距离)的两座城市，A，B分别位于河的两岸(假定岸是平行的直线)，现需铺设一条电缆连通A与B，已知地下电缆的修建费为每千米2万元，水下电缆的修建费为每千米4万元，问应如何铺设电缆可使总的修建费用最少？(＝1.732，＝2.236，＝3.8730)