数列{a_n}的前n项和S_n满足log_a(S_n+a)=n+1(a>0,a1),则此数列的通项公式为  

若对任意的n∈N*,总有a_n<a_n+1,则称{a_n}为递增数列，现有下列命题：

①公比q>1的等比数列是递增数列.②若d>0，则等差数列为递增数列.③若a₁>0,q>0，则等比数列为递增数列。

其中真命题的序号为____________.

①公比q>1的等比数列是递增数列.②若d>0，则等差数列为递增数列.③若a₁>0,q>0，则等比数列为递增数列。

其中真命题的序号为____________.

(本题满分16分)已知二次函数f (x) = x² ??ax + a (x∈R)同时满足：①不等式 f (x) ≤ 0的解集有且只有一个元素；②在定义域内存在0 < x₁ < x₂，使得不等式f (x₁) > f (x₂)成立．设数列{a_n}的前 n 项和S_n = f (n)．（1）求函数f (x)的表达式；（2）求数列{a_n}的通项公式；（3）在各项均不为零的数列{c_n}中，若c_i·c_i+1 < 0，则称c_i，c_i+1为这个数列{c_n}一对变号项．令c_n = 1 ?? （n为正整数），求数列{c_n}的变号项的对数．

1．   (本小题满分13分)

已知数列{a_n}有a₁ = a，a₂ = p（常数p > 0），对任意的正整数n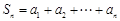，，且．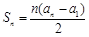

(1) 求a的值；

(2) 试确定数列{a_n}是否是等差数列，若是，求出其通项公式；若不是，说明理由；

(3) 对于数列{b_n}，假如存在一个常数b，使得对任意的正整数n都有b_n< b，且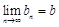，则称b为数列{b_n}的“上渐近值”，令，求数列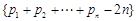的“上渐近值”．