
题目列表(包括答案和解析)
(本题12分)函数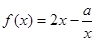 的定义域为
的定义域为 ,
,
(1)若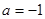 ,求函数
,求函数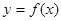 的值域;
的值域;
(2)求函数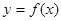 在
在 上的最大值和最小值,并求出函数取最值时相应
上的最大值和最小值,并求出函数取最值时相应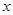 的值。
的值。
.(本题12分)已知函数
 的图象与x轴交点为
的图象与x轴交点为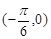 ,相邻最高点坐标为
,相邻最高点坐标为 .
.
(1)求函数 的表达式;
的表达式;
(2)求函数 的单调增区间;
的单调增区间;
(3)求函数 在
在 上的最值.
上的最值.
(本题满分12分)
已知数列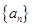 的前
的前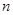 和为
和为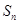 ,其中
,其中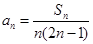 且
且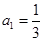
(1)求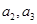
(2)猜想数列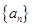 的通项公式,并用数学归纳法加以证明.
的通项公式,并用数学归纳法加以证明.
(本题12分)已知⊙O:![]() 和定点A(2,1),⊙O外一点
和定点A(2,1),⊙O外一点![]() 向⊙O引切线PQ ,切点为Q ,且满足
向⊙O引切线PQ ,切点为Q ,且满足![]() .
.
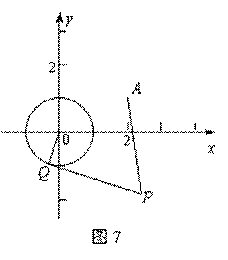 (1) 求实数
(1) 求实数![]() 间满足的等量关系;
间满足的等量关系;
(2) 求线段PQ长的最小值;
(3) 若以P为圆心所作的⊙P与⊙O有公共点,
试求:半径取最小值时⊙P的方程.
(本题12分)2011年初为遏制商品房价格上涨速度过快增长,国务院要求各地邀出台相 应措施。 继北京、上海、深圳、杭州等城市出台楼市“限购令”后,1月21日,南昌版“限购令”正式公布,将于2月1日起施行。某校一课题小组对南昌市工薪阶层对“楼市限购令”态度进行调查,抽调了50人,他们月收入频数分别表急对“楼市限购令”赞成人数如下表。
| 月收入 (单位:百元) |
|
|
|
|
|
|
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成人数 | 4 | 8 | 12 | 5 | 3 | 1 |
(1)完成下图的月收入频率分布直方图(注意填写纵坐标)及2×2列联表;
| 月收入不低于55百元人数 | 月收入低于55百元人数 | 合计 | |
| 赞成 |
|
| |
| 不赞成 |
|
| |
| 合计 |

(2)若从收入(单位:百元)在![]() 的被调查者中随机选取两人进行追踪调查,求选中的2人恰好有1人不赞成“楼市限购令”的概率.
的被调查者中随机选取两人进行追踪调查,求选中的2人恰好有1人不赞成“楼市限购令”的概率.
(3)请回答研究被调查者“收入与赞成”是否有90%以上的把握。
 参考数据:
参考数据:
![]() 时有90%把握认为A与B有关
时有90%把握认为A与B有关
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com