函数，方程的两个根分别为1和4.

（Ⅰ）当 a_{=3且曲线过原点时，求的解析式。}

（Ⅱ）若在无极值点，求a的取值范围_．

(本小题满分12分)

已知是首项为19，公差为-2的等差数列，为的前项和.

（1）当n为何值时最大（用两种方法）；

（2）设是首项为1，公比为3的等比数列，求数列的通项公式及其前项和。

设A是如下形式的2行3列的数表，

满足性质P：a，b，c，d，e，f，且a+b+c+d+e+f=0

记为A的第i行各数之和（i=1,2）, 为A的第j列各数之和（j=1,2,3）记为中的最小值。

（1）对如下表A，求的值

(2)设数表A形如

其中，求的最大值

（3）对所有满足性质P的2行3列的数表A，求的最大值。

【解析】（1）因为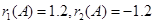，，所以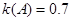

（2），

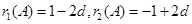因为，所以，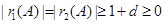

所以

当d=0时，取得最大值1

（3）任给满足性质P的数表A（如图所示）

任意改变A的行次序或列次序，或把A中的每个数换成它的相反数，所得数表仍满足性质P，并且，因此，不妨设，，

由得定义知，，，，

从而

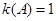所以，，由（2）知，存在满足性质P的数表A使，故的最大值为1

【考点定位】此题作为压轴题难度较大，考查学生分析问题解决问题的能力，考查学生严谨的逻辑思维能力

（本小题共12分） 在平面直角坐标系中,已知A_n(n,a_n)、B_n(n,b_n)、C_n(n-1,0)(n∈N*)，满足向量与向量共线，且点A_n(n,a_n) (n∈N*)都在斜率为2的同一条直线l上. 若a₁=-3，b₁=10　（1）求数列{a_n}与{ b_n }的通项公式；

（2）求当n取何值时△A_nB_nC_n的面积S_n最小，并求出S_n的这个最小值。 

设函数定义域为，当时,,且对于任意的,都有 

（1）求的值,并证明函数在上是减函数；

（2）记△ABC的三内角A、B、C的对应边分别为a，b，c，若时，不等式恒成立，求实数的取值范围。