
题目列表(包括答案和解析)
A、(-
| ||
| B、(0,+∞) | ||
| C、[-2,+∞) | ||
| D、(-3,+∞) |
A.(-![]() ,+∞) B.(0,+∞) C.(-2,+∞) D.(-3,+∞)
,+∞) B.(0,+∞) C.(-2,+∞) D.(-3,+∞)
已知{an}是递增数列,且对任意n∈N*都有an=n2+λn恒成立,则实数λ的取值范围是( ).
A.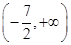 B.(0,+∞) C.(-2,+∞) D.(-3,+∞)
B.(0,+∞) C.(-2,+∞) D.(-3,+∞)
已知{an}是递增数列,且对任意n∈N*都有an=n2+λn恒成立,则实数λ的取值范围是( )
A.(-,+∞) B.(0,+∞) C.[-2,+∞) D.(-3,+∞)
已知{an}是递增数列,且对任意n∈N*都有an=n2+λn恒成立,则实数λ的取值范围是( )
A.(-,+∞) B.(0,+∞) C.[-2,+∞) D.(-3,+∞)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com