设f(x)= 的反函数为f-1(x)=ax-5.那么a.b的值分别是( ) A.2. B..2 C. D.-5. 【
查看更多】
题目列表(包括答案和解析)
由函数y=f(x)确定数列{a
n},a
n=f(n),函数y=f(x)的反函数y=f
-1(x)能确定数列b
n,b
n=f
-1(n)若对于任意n∈N
*都有b
n=a
n,则称数列{b
n}是数列{a
n}的“自反函数列”
(1)设函数f(x)=
,若由函数f(x)确定的数列{a
n}的自反数列为{b
n},求a
n;
(2)已知正整数列{c
n}的前项和s
n=
(c
n+
).写出S
n表达式,并证明你的结论;
(3)在(1)和(2)的条件下,d
1=2,当n≥2时,设d
n=
,D
n是数列{d
n}的前n项和,且D
n>log
a(1-2a)恒成立,求a的取值范围.
查看答案和解析>>
由函数y=f(x)确定数列{a
n},a
n=f(n),函数y=f(x)的反函数y=f
-1(x)能确定数列b
n,b
n=f
-1(n)若对于任意n∈N
*都有b
n=a
n,则称数列{b
n}是数列{a
n}的“自反函数列”
(1)设函数f(x)=
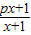
,若由函数f(x)确定的数列{a
n}的自反数列为{b
n},求a
n;
(2)已知正整数列{c
n}的前项和s
n=

(c
n+
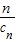
).写出S
n表达式,并证明你的结论;
(3)在(1)和(2)的条件下,d
1=2,当n≥2时,设d
n=
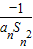
,D
n是数列{d
n}的前n项和,且D
n>log
a(1-2a)恒成立,求a的取值范围.
查看答案和解析>>
由函数y=f(x)确定数列{a
n},a
n=f(n),函数y=f(x)的反函数y=f
-1(x)能确定数列b
n,b
n=f
-1(n)若对于任意n∈N
*都有b
n=a
n,则称数列{b
n}是数列{a
n}的“自反函数列”
(1)设函数f(x)=
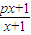
,若由函数f(x)确定的数列{a
n}的自反数列为{b
n},求a
n;
(2)已知正整数列{c
n}的前项和s
n=

(c
n+
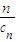
).写出S
n表达式,并证明你的结论;
(3)在(1)和(2)的条件下,d
1=2,当n≥2时,设d
n=
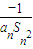
,D
n是数列{d
n}的前n项和,且D
n>log
a(1-2a)恒成立,求a的取值范围.
查看答案和解析>>
由函数y=f(x)确定数列{a
n},a
n=f(n),函数y=f(x)的反函数y=f
-1(x)能确定数列b
n,b
n=f
-1(n)若对于任意n∈N
*都有b
n=a
n,则称数列{b
n}是数列{a
n}的“自反函数列”
(1)设函数f(x)=

,若由函数f(x)确定的数列{a
n}的自反数列为{b
n},求a
n;
(2)已知正整数列{c
n}的前项和s
n=

(c
n+

).写出S
n表达式,并证明你的结论;
(3)在(1)和(2)的条件下,d
1=2,当n≥2时,设d
n=

,D
n是数列{d
n}的前n项和,且D
n>log
a(1-2a)恒成立,求a的取值范围.
查看答案和解析>>
由函数y=f(x)确定数列{a
n},a
n=f(n),函数y=f(x)的反函数y=f
-1(x)能确定数列b
n,b
n=f
-1(n)若对于任意n∈N
*都有b
n=a
n,则称数列{b
n}是数列{a
n}的“自反函数列”
(1)设函数f(x)=
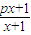
,若由函数f(x)确定的数列{a
n}的自反数列为{b
n},求a
n;
(2)已知正整数列{c
n}的前项和s
n=

(c
n+
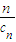
).写出S
n表达式,并证明你的结论;
(3)在(1)和(2)的条件下,d
1=2,当n≥2时,设d
n=
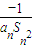
,D
n是数列{d
n}的前n项和,且D
n>log
a(1-2a)恒成立,求a的取值范围.
查看答案和解析>>

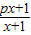 ,若由函数f(x)确定的数列{an}的自反数列为{bn},求an;
,若由函数f(x)确定的数列{an}的自反数列为{bn},求an; (cn+
(cn+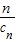 ).写出Sn表达式,并证明你的结论;
).写出Sn表达式,并证明你的结论;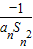 ,Dn是数列{dn}的前n项和,且Dn>loga(1-2a)恒成立,求a的取值范围.
,Dn是数列{dn}的前n项和,且Dn>loga(1-2a)恒成立,求a的取值范围.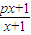 ,若由函数f(x)确定的数列{an}的自反数列为{bn},求an;
,若由函数f(x)确定的数列{an}的自反数列为{bn},求an; (cn+
(cn+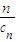 ).写出Sn表达式,并证明你的结论;
).写出Sn表达式,并证明你的结论;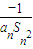 ,Dn是数列{dn}的前n项和,且Dn>loga(1-2a)恒成立,求a的取值范围.
,Dn是数列{dn}的前n项和,且Dn>loga(1-2a)恒成立,求a的取值范围. ,若由函数f(x)确定的数列{an}的自反数列为{bn},求an;
,若由函数f(x)确定的数列{an}的自反数列为{bn},求an; (cn+
(cn+ ).写出Sn表达式,并证明你的结论;
).写出Sn表达式,并证明你的结论; ,Dn是数列{dn}的前n项和,且Dn>loga(1-2a)恒成立,求a的取值范围.
,Dn是数列{dn}的前n项和,且Dn>loga(1-2a)恒成立,求a的取值范围.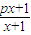 ,若由函数f(x)确定的数列{an}的自反数列为{bn},求an;
,若由函数f(x)确定的数列{an}的自反数列为{bn},求an; (cn+
(cn+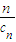 ).写出Sn表达式,并证明你的结论;
).写出Sn表达式,并证明你的结论;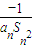 ,Dn是数列{dn}的前n项和,且Dn>loga(1-2a)恒成立,求a的取值范围.
,Dn是数列{dn}的前n项和,且Dn>loga(1-2a)恒成立,求a的取值范围.