
题目列表(包括答案和解析)
已知二次函数f(x)的图象过A(-1,0)、B(3,0)、C(1,-8).
(1)求f(x)的解析式
(2)画f(x)的图象,并由图象给出该函数的值域
(3)求不等式f(x)≥0的解集
(4)将f(x)的图象向右平移2个单位,求所得图象的函数解析式
已知正三角形ABC的顶点A(1,1),B(1,3),顶点C在第一象限,若点(x,y)在△ABC内部,则z=-x+y的取值范围是
(A)(1- ,2) (B)(0,2)
(C)(
,2) (B)(0,2)
(C)( -1,2) (D)(0,1+
-1,2) (D)(0,1+ )
)
【解析】 做出三角形的区域如图 ,由图象可知当直线
,由图象可知当直线 经过点B时,截距最大,此时
经过点B时,截距最大,此时 ,当直线经过点C时,直线截距最小.因为
,当直线经过点C时,直线截距最小.因为 轴,所以
轴,所以 ,三角形的边长为2,设
,三角形的边长为2,设 ,则
,则 ,解得
,解得 ,
, ,因为顶点C在第一象限,所以
,因为顶点C在第一象限,所以 ,即
,即 代入直线
代入直线 得
得 ,所以
,所以 的取值范围是
的取值范围是 ,选A.
,选A.
| a |
| π |
| 4 |
| b |
| a |
| b |
| π |
| 4 |

(1)求函数f(x)的最大值、最小值及单调增区间;
(2)函数f(x)的图象是由函数y=sinx,x∈R的图象经过怎样的变换而得到的?
分析:解此类问题的关键是把函数f(x)转化成一个角的一个三角函数的形式.
已知函数 。
。
(1)求函数的最小正周期和最大值;
(2)求函数的增区间;
(3)函数的图象可以由函数 的图象经过怎样的变换得到?
的图象经过怎样的变换得到?
【解析】本试题考查了三角函数的图像与性质的运用。第一问中,利用 可知函数的周期为
可知函数的周期为 ,最大值为
,最大值为 。
。
第二问中,函数 的单调区间与函数
的单调区间与函数 的单调区间相同。故当
的单调区间相同。故当 ,解得x的范围即为所求的区间。
,解得x的范围即为所求的区间。
第三问中,利用图像将 的图象先向右平移
的图象先向右平移 个单位长度,再把横坐标缩短为原来的
个单位长度,再把横坐标缩短为原来的 (纵坐标不变),然后把纵坐标伸长为原来的
(纵坐标不变),然后把纵坐标伸长为原来的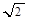 倍(横坐标不变),再向上平移1个单位即可。
倍(横坐标不变),再向上平移1个单位即可。
解:(1)函数 的最小正周期为
的最小正周期为 ,最大值为
,最大值为 。
。
(2)函数 的单调区间与函数
的单调区间与函数 的单调区间相同。
的单调区间相同。
 即
即
 所求的增区间为
所求的增区间为 ,
,
 即
即
 所求的减区间为
所求的减区间为 ,
, 。
。
(3)将 的图象先向右平移
的图象先向右平移 个单位长度,再把横坐标缩短为原来的
个单位长度,再把横坐标缩短为原来的 (纵坐标不变),然后把纵坐标伸长为原来的
(纵坐标不变),然后把纵坐标伸长为原来的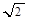 倍(横坐标不变),再向上平移1个单位即可。
倍(横坐标不变),再向上平移1个单位即可。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com