
题目列表(包括答案和解析)
(本小题满分10分)一架飞机从A地飞到B到,两地相距700km.飞行员为了避开某一区域的雷雨云层,从机场起飞后,就沿与原来的飞行方向成 角的方向飞行,飞行到中途,再沿与原来的飞行方向成
角的方向飞行,飞行到中途,再沿与原来的飞行方向成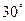 夹角的方向继续飞行
夹角的方向继续飞行 直到终点.这样飞机的飞行路程比原来路程700km远了多少?(
直到终点.这样飞机的飞行路程比原来路程700km远了多少?( )
)
|
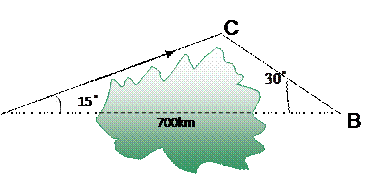
一架飞机从A地飞到B到,两地相距700km.飞行员为了避开某一区域的雷雨云层,从机场起飞后,就沿与原来的飞行方向成 角的方向飞行,飞行到中途,再沿与原来的飞行方向成
角的方向飞行,飞行到中途,再沿与原来的飞行方向成 夹角的方向继续飞行直到终点.这样飞机的飞行路程比原来路程700km远了多少?
夹角的方向继续飞行直到终点.这样飞机的飞行路程比原来路程700km远了多少?
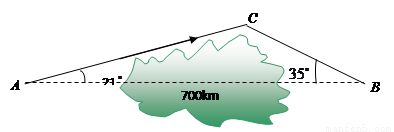
一架飞机从A地飞到B到,两地相距700km.飞行员为了避开某一区域的雷雨云层,从机场起飞后,就沿与原来的飞行方向成![]() 角的方向飞行,飞行到中途,再沿与原来的飞行方向成
角的方向飞行,飞行到中途,再沿与原来的飞行方向成![]() 夹角的方向继续飞行直到终点.这样飞机的飞行路程比原来路程700km远了多少?
夹角的方向继续飞行直到终点.这样飞机的飞行路程比原来路程700km远了多少?
 |
一架飞机从A地飞到B到,两地相距700 km.飞行员为了避开某一区域的雷雨云层,从机场起飞后,就沿与原来的飞行方向成15°角的方向飞行,飞行到中途,再沿与原来的飞行方向成30°夹角的方向继续飞行直到终点.这样飞机的飞行路程比原来路程700 km远了多少?(![]() m.)
m.)
下列关于算法的几种说法中正确的是
算法就是某一个问题的解题方法
解决某一问题的算法不唯一
一个算法可以不产生确定的结果
算法可以无限地执行下去
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com