
题目列表(包括答案和解析)
| a |
| b |
| c |
| 0 |
| a |
| b |
| c |
| A、都是非零向量时也可能无法构成一个三角形 |
| B、一定不可能构成三角形 |
| C、都是非零向量时能构成三角形 |
| D、一定可构成三角形 |
在下列判断中,正确的是( )
①长度为0的向量都是零向量;
②零向量的方向都是相同的;
③单位向量的长度都相等;
④单位向量都是同方向;
⑤任意向量与零向量都共线.
A.①②③ B.②③④
C.①②⑤ D.①③⑤
已知a,b是非零向量且满足(a-2b)⊥a,(b-2a)⊥b,则a与b的夹角是( )
A ![]() B
B ![]() C
C ![]() D
D ![]()
已知非零向量 ,
,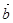 满足
满足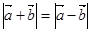 ,则
,则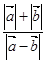 的取值范围是( )
的取值范围是( )
A.  B.
B. 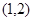 C.
C. 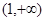 D.
D. 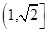
下列命题:
①相等的向量,它们的坐标相等;反之,若数轴上两个向量的坐标相等,则这两个向量相等;
②对于任何一个实数,数轴上存在一个确定的点与之对应;
③数轴上向量![]() 的坐标是一个数,实数的绝对值为线段AB的长度,如果起点指向终点的方向与数轴同方向,则这个实数取正数,反之取负数;
的坐标是一个数,实数的绝对值为线段AB的长度,如果起点指向终点的方向与数轴同方向,则这个实数取正数,反之取负数;
④起点和终点重合的向量是零向量,它的方向是任意的,它的坐标是0.
其中正确命题的个数是( )
A.1 B.2 C.3 D.4
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com