
题目列表(包括答案和解析)
| n |
材料:采访零向量
W:你好!零向量.我是《数学天地》的一名记者,为了让在校的高中生更好了解你,能不能对你进行一次采访呢?
零向量:当然可以,我们向量王国随时恭候大家的光临,很乐意接受你的采访,让高中生朋友更加了解我,更好地为他们服务.
W:好的,那就开始吧!你的名字有什么特殊的含义吗?
零向量:零向量就是长度为零的向量,它与数字0有着密切的联系,所以用0来表示我.
W:你与其他向量有什么共同之处呢?
零向量:既然我是向量王国的一个成员,就具有向量的基本性质,如既有大小又有方向,在进行加、减法运算时满足交换律和结合律,还定义了与实数的积.
W:你有哪些值得骄傲的特殊荣耀呢?
零向量:首先,我的方向是不定的,可以与任意的向量平行.其次,我还有其他一些向量所没有的特殊待遇:如我的相反向量仍是零向量;在向量的线性运算中,我与实数0很有相似之处.
W:你有如此多的荣耀,那么是否还有烦恼之事呢?
零向量:当然有了,在向量王国还有许多“权利和义务”却大有把我排斥在外之意,如平行向量的定义,向量共线定理,两向量夹角的定义都对我进行了限制.所有这些确实给一些高中生带来了很多苦恼,在此我向大家真诚地说一声:对不起,这不是我的错.但我还是很高兴有这次机会与大家见面.
W:OK!采访就到这里吧,非常感谢你的合作,再见!
零向量:Bye!
阅读上面的材料回答下面问题.
应用零向量时应注意哪些问题?
| e1 |
| e2 |
| a |
| a |
| e1 |
| e2 |
| a |
| i |
| j |
| i |
| j |
| π |
| 3 |
| i |
| j |
| a |
如图,在平面斜坐标系xOy中,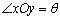 ,平面上任意一点P关于斜坐标系的斜坐标这样定义:若
,平面上任意一点P关于斜坐标系的斜坐标这样定义:若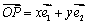 (其中
(其中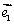 ,
,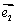 分别是x轴,y轴正方向的单位向量),则P点的斜坐标为(x,y),向量
分别是x轴,y轴正方向的单位向量),则P点的斜坐标为(x,y),向量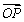 的斜坐标为(x,y).给出以下结论:
的斜坐标为(x,y).给出以下结论:
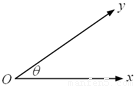
①若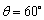 ,P(2,-1),则
,P(2,-1),则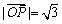 ;
;
②若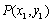 ,
,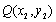 ,则
,则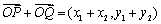 ;
;
③若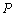 (x,y),
(x,y),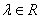 ,则
,则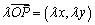 ;
;
④若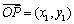 ,
,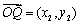 ,则
,则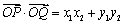 ;
;
⑤若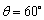 ,以O为圆心,1为半径的圆的斜坐标方程为
,以O为圆心,1为半径的圆的斜坐标方程为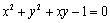 .
.
其中所有正确的结论的序号是______________.
| e1 |
| e2 |
| a |
| a |
| e1 |
| e2 |
| a |
| i |
| j |
| i |
| j |
| π |
| 3 |
| i |
| j |
| a |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com