练习册

  • 练习册
  • 试题
    大家首先回顾一下两角和的正弦.余弦和正切公式. ,, ． 思考:当=这些公式会变成怎么样呢? 【查看更多】

     

    题目列表(包括答案和解析)

    从特殊到一般和从一般到特殊，这是人们正确认识客观事物的认识规律，也是处理数学问题的重要思想方法.从这一思想出发，我们知道两角和的正弦为：sin（α+β）=sinαcosβ+cosαsinβ，那么现在我们令α=β，在这种特殊情况下我们可以得到公式sin2α=2sinαcosα，同理其余几种三角函数也可以做类似的推理，本节我们就来研究一下有关倍角的公式.你能利用上述知识解决下面的问题吗？

    已知sinα=，α∈（，π），求sin2α，cos2α，tan2α的值.

    查看答案和解析>>

    类比有关“两角和与差的正弦、余弦公式”的形式，对给定的两个函数S(x)=
    ax-a-x
    2
    ，C(x)=
    ax+a-x
    2
    其中a＞0，且a≠1，请写出一个关于S（x）和C（x）的运算公式：
    S（x+y）=S（x）C（y）+S（y）C（x），或S（x-y）=S（x）C（y）-S（y）C（x）等
    S（x+y）=S（x）C（y）+S（y）C（x），或S（x-y）=S（x）C（y）-S（y）C（x）等
    ．

    查看答案和解析>>

    阅读下面材料：
    根据两角和与差的正弦公式，有
    sin（α+β）=sinαcosβ+cosαsinβ------①
    sin（α-β）=sinαcosβ-cosαsinβ------②
    由①+②得sin（α+β）+sin（α-β）=2sinαcosβ------③
    α+β=A，α-β=B 有α=
    A+B
    2
    ，β=
    A-B
    2

    代入③得 sinA+cosB=2sin
    A+B
    2
    cos
    A-B
    2
    ．
    （1）类比上述推理方法，根据两角和与差的余弦公式，证明：cosA-cosB=-2sin
    A+B
    2
    sin
    A-B
    2
    ；
    （2）若△ABC的三个内角A，B，C满足cos2A+cox2C-cos2B=1，直接利用阅读材料及（1）中的结论试判断△ABC的形状．

    查看答案和解析>>

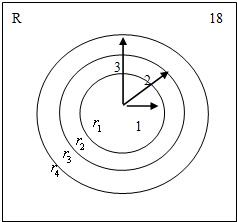    精英家教网山姆的意大利馅饼屋中设有一个投镖靶 该靶为正方形板．边长为18厘米，挂于前门附近的墙上，顾客花两角伍分的硬币便可投一镖并可有机会赢得一种意大利 馅饼中的一个，投镖靶中画有三个同心圆，圆心在靶的中心，当投镖击中半径为1厘米的最内层圆域时．可得到一个大馅饼；当击中半径为1厘米到2厘米之间的环域时，可得到一个中馅饼；如果击中半径为2厘米到3厘米之间的环域时，可得到一个小馅饼，如果击中靶上的其他部分，则得不到谄饼，我们假设每一个顾客都能投镖中靶，并假设每个圆的周边线没有宽度，即每个投镖不会击中线上，试求一顾客将嬴得：
    （1）一张大馅饼的概率；
    （2）一张中馅饼的概率；
    （3）一张小馅饼的概率；
    （4）没得到馅饼的概率．

    查看答案和解析>>

    （Ⅰ）①证明两角和的余弦公式Cα+β：cos（α+β）=cosαcosβ-sinαsinβ；②由Cα+β推导两角和的正弦公式Sα+β：sin（α+β）=sinαcosβ+cosαsinβ．
    （Ⅱ）已知△ABC的面积S=
    1
    2
    ，
    AB
    •
    AC
    =3    ，且cosB=
    3
    5
    ，求cosC．

    查看答案和解析>>


    同步练习册答案