
题目列表(包括答案和解析)
| a |
| b |
| a |
| b |
| a |
| b |
| p |
| π |
| 2 |
| AB |
| p |
| AB |
| 5 |
| OA |
| OB |
| AC |
| p |
| OA |
| OC |
| p |
| π |
| 2 |
| AB |
| p |
| AB |
| 5 |
| OA |
| OB |
| AC |
| p |
| OA |
| OC |
(1)求与向量a=(2,-1,2)共线且满足方程a·x=-18的向量x的坐标;
(2)已知A、B、C三点坐标分别为(2,-1,2),(4,5,-1),(-2,2,3),求点P的坐标使得![]() =
=![]() (
(![]() -
-![]() );
);
(3)已知a=(3,5,-4),b=(2,1,8),求:①a·b;②a与b夹角的余弦值;
③确定![]() ,
,![]() 的值使得
的值使得![]() a+
a+![]() b与z轴垂直,且(
b与z轴垂直,且(![]() a+
a+![]() b)·(a+b)=53.
b)·(a+b)=53.
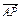 =
=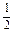 (
(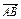 -
-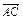 );
);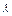 ,
,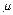 的值使得
的值使得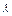 a+
a+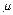 b与z轴垂直,且(
b与z轴垂直,且(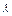 a+
a+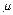 b)·(a+b)=53.
b)·(a+b)=53.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com