
题目列表(包括答案和解析)
(1)已知角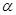 的顶点在原点,始边与x轴正半轴重合,终边为射线4x+3y=0(x≥0),求5sin
的顶点在原点,始边与x轴正半轴重合,终边为射线4x+3y=0(x≥0),求5sin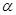 -3 tan
-3 tan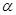 +2cos
+2cos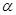 的值.
的值.
(2)化简: .其中
.其中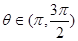 .
.
将边长为1的正三角形![]() 按如图所示的方式放置,其中顶点
按如图所示的方式放置,其中顶点![]() 与坐标原点重合.记边
与坐标原点重合.记边![]() 所在直线的倾斜角为
所在直线的倾斜角为![]() ,已知
,已知![]() .
.
(Ⅰ)试用![]() 表示
表示![]() 的坐标(要求将结果化简为形如
的坐标(要求将结果化简为形如![]() 的形式);
的形式);
(Ⅱ)定义:对于直角坐标平面内的任意两点![]() 、
、![]() ,称
,称![]() 为
为![]() 、
、![]() 两点间的“taxi距离” ,并用符号
两点间的“taxi距离” ,并用符号![]() 表示.试求
表示.试求![]() 的最大值.
的最大值.
 |
将边长为1的正三角形![]() 按如图所示的方式放置,其中顶点
按如图所示的方式放置,其中顶点![]() 与坐标原点重合.记边
与坐标原点重合.记边![]() 所在直线的倾斜角为
所在直线的倾斜角为![]() ,已知
,已知![]() .
.
(Ⅰ)试用![]() 表示
表示![]() 的坐标(要求将结果化简为形如
的坐标(要求将结果化简为形如![]() 的形式);
的形式);
(Ⅱ)定义:对于直角坐标平面内的任意两点![]() 、
、![]() ,称
,称![]() 为
为![]() 、
、![]() 两点间的“taxi距离” ,并用符号
两点间的“taxi距离” ,并用符号![]() 表示.试求
表示.试求![]() 的最大值.
的最大值.
 |
将边长为1的正三角形![]() 按如图所示的方式放置,其中顶点
按如图所示的方式放置,其中顶点![]() 与坐标原点重合.记边
与坐标原点重合.记边![]() 所在直线的倾斜角为
所在直线的倾斜角为![]() ,已知
,已知![]() .
.
(Ⅰ)试用![]() 表示
表示![]() 的坐标(要求将结果化简为形如
的坐标(要求将结果化简为形如![]() 的形式);
的形式);
(Ⅱ)定义:对于直角坐标平面内的任意两点![]() 、
、![]() ,称
,称![]() 为
为![]() 、
、![]() 两点间的“taxi距离” ,并用符号
两点间的“taxi距离” ,并用符号![]() 表示.试求
表示.试求![]() 的最大值.
的最大值.
 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com