
题目列表(包括答案和解析)
(本小题满分为12分)
某中学研究性学习小组,为了考察高中学生的作文水平与爱看课外书的关系,在本校高三年级随机调查了 名学生。调査结果表明:在爱看课外书的
名学生。调査结果表明:在爱看课外书的 人中有
人中有 人作文水平好,另
人作文水平好,另 人作文水平一般;在不爱看课外书的
人作文水平一般;在不爱看课外书的 人中有
人中有 人作文水平好,另
人作文水平好,另 人作文水平一般.
人作文水平一般.
(Ⅰ)试根据以上数据建立一个 列联表,并运用独立性检验思想,指出有多大把握认为中学生的作文水平与爱看课外书有关系?
列联表,并运用独立性检验思想,指出有多大把握认为中学生的作文水平与爱看课外书有关系?
(Ⅱ)将其中某5名爱看课外书且作文水平好的学生分别编号为 ,某
,某 名爱看课外书且作文水平一般的学生也分别编号为
名爱看课外书且作文水平一般的学生也分别编号为 ,从这两组学生中各任选
,从这两组学生中各任选 人进行学习交流,求被选取的两名学生的编号之和为
人进行学习交流,求被选取的两名学生的编号之和为 的倍数或
的倍数或 的倍数的概率.
的倍数的概率.
附:
临界值表:
|
|
0. 10 |
0. 05 |
0. 025 |
0.010 |
0. 005 |
0. 001 |
|
|
2. 706 |
3. 841 |
5. 024 |
6. 635 |
7. 879 |
10. 828 |
(本小题满分为12分)
已知函数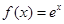 ,其图像在点
,其图像在点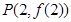 处的切线为
处的切线为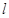 .
.
(1)求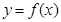 、直线
、直线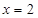 及两坐标轴围成的图形绕
及两坐标轴围成的图形绕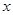 轴旋转一周所得几何体的体积;
轴旋转一周所得几何体的体积;
(2)求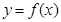 、直线
、直线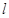 及
及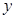 轴围成图形的面积.
轴围成图形的面积.
(本小题满分为14分)
已知抛物线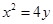 的焦点为F,A、B是热线上的两动点,且
的焦点为F,A、B是热线上的两动点,且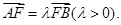 过A、B两点分别作抛物线的切线,设其交点为M。
过A、B两点分别作抛物线的切线,设其交点为M。
(I)证明 为定值;
为定值;
(II)设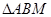 的面积为S,写出
的面积为S,写出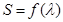 的表达式,并求S的最小值。
的表达式,并求S的最小值。
(本小题满分为12分)如图某河段的两岸可视为平行,为了测量该河段的宽度,在河段的一岸边选取两点 ,观察对岸的点
,观察对岸的点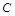 ,测得
,测得 ,
, ,且
,且 米.
米.

(1)求 ;
;
(2)求该河段的宽度.
(本小题满分为14分)定义在(-1,1)上的函数 满足:
满足:
①对任意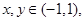 都有
都有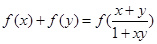 ;
;
② 在
在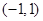 上是单调递增函数,
上是单调递增函数,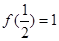 .
.
(1)求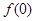 的值;
的值;
(2)证明 为奇函数;
为奇函数;
(3)解不等式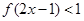 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com