
题目列表(包括答案和解析)
| 5 |
| 2 |
| 13 |
| 2 |
|
| b2 |
| 2 |
| bn |
| n |
| 17 |
| 12 |
 n2-
n2- n(n∈N*),试证明{△an}是等差数列;
n(n∈N*),试证明{△an}是等差数列; ,求证:b1+
,求证:b1+ +…+
+…+ <
< .
. n2-
n2- n(n∈N*),试证明{△an}是等差数列;
n(n∈N*),试证明{△an}是等差数列;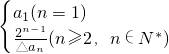 ,求证:b1+
,求证:b1+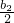 +…+
+…+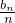 <
<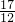 .
.有限集合
A的元素个数记作card(A).如A={a,b,c,d},则card(A)=4.一般地,对于任意两个集合A、B,有:card(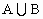 )=card(A)
)=card(A)
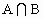 ).
).
两个变形公式为:
card(A)
+card(B)=card(A∪B)+card(A∩B);card(A
∩B)=card(A)+card(B)-card(A∪B).请根据以上知识解下题.
学校举办了一次田径运动会,某班有
8名同学参赛,又举办了一次球类运动会,这个班有12名同学参赛,两次运动会都参赛的有3人.两次运动会中,这个班共有多少名同学参赛?有限集合A的元素个数记作card(A).如A={a,b,c,d},则card(A)=4.一般地,对于任意两个集合A、B,有:
card(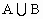 )=card(A)+card(B)-card(
)=card(A)+card(B)-card(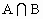 ).
).
两个变形公式为:
card(A)+card(B)=card(A∪B)+card(A∩B);
card(A∩B)=card(A)+card(B)-card(A∪B).
请根据以上知识解下题.
学校举办了一次田径运动会,某班有8名同学参赛,又举办了一次球类运动会,这个班有12名同学参赛,两次运动会都参赛的有3人.两次运动会中,这个班共有多少名同学参赛?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com