
题目列表(包括答案和解析)
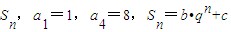 (q≠0,q≠±1,bc≠0,b+c=0),现把数列{an}的各项排成如图所示的三角形形状.记A(m,n)为第m行从左起第n个数(m、n∈N*).有下列命题:
(q≠0,q≠±1,bc≠0,b+c=0),现把数列{an}的各项排成如图所示的三角形形状.记A(m,n)为第m行从左起第n个数(m、n∈N*).有下列命题: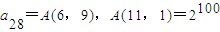 ;
; ,
,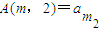 …
…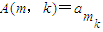 ,其中
,其中 为A(m,n)的最大值,从所有m1,m2,m3,…,mk中任取一个数,若取得的数恰好为奇数的概率为
为A(m,n)的最大值,从所有m1,m2,m3,…,mk中任取一个数,若取得的数恰好为奇数的概率为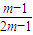 ,则m必然为偶数.
,则m必然为偶数.
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
| 3 |
| OM |
| ON |
| OQ |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com