
题目列表(包括答案和解析)
 (2012•湖南模拟)选做题(请考生在第16题的三个小题中任选两题作答,如果全做,则按前两题记分,要写出必要的推理与演算过程)
(2012•湖南模拟)选做题(请考生在第16题的三个小题中任选两题作答,如果全做,则按前两题记分,要写出必要的推理与演算过程)
|
| a2 |
| x |
| b2 |
| y |
| (a+b)2 |
| x+y |
| a |
| x |
| b |
| y |
| 2 |
| x |
| 9 |
| 1-2x |
| 1 |
| 2 |
|
|
关于统计数据的分析,有以下几个结论,其中正确的个数为( )
①利用残差进行回归分析时,若残差点比较均匀地落在宽度较窄的水平带状区域内,则说明线性回归模型的拟合精度较高;
②将一组数据中的每个数据都减去同一个数后,期望与方差均没有变化;
③调查剧院中观众观后感时,从50排(每排人数相同)中任意抽取一排的人进行调查是分层抽样法;
④已知随机变量X服从正态分布N(3,1),且P(2≤X≤4)=0.682 6,则P(X>4)等于0.158 7
⑤某单位有职工750人,其中青年职工350人,中年职工250人,老年职工150人.为了了解该单位职工的健康情况,用分层抽样的方法从中抽取样本.若样本中的青年职工为7人,则样本容量为15人。
A.2 B.3 C.4 D.5
 选做题(请考生在第16题的三个小题中任选两题作答,如果全做,则按前两题记分,要写出必要的推理与演算过程)
选做题(请考生在第16题的三个小题中任选两题作答,如果全做,则按前两题记分,要写出必要的推理与演算过程)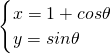 (θ为参数),求曲线C上的点到直线x-y+1=0的距离的最大值.
(θ为参数),求曲线C上的点到直线x-y+1=0的距离的最大值.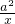 +
+ ≥
≥ ,当且仅当
,当且仅当 =
=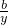 时上式取等号.请利用以上结论,求函数f(x)=
时上式取等号.请利用以上结论,求函数f(x)= +
+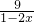 (x∈0,
(x∈0, )的最小值.
)的最小值.(本题满分12分)已知函数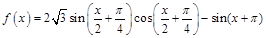 。
。
(1)求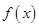 的最小正周期;
的最小正周期;
(2)若将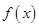 的图象向右平移
的图象向右平移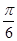 个单位,得到函数
个单位,得到函数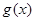 的图象,求函数
的图象,求函数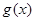 在区间
在区间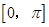 上的最大值和最小值。
上的最大值和最小值。
【解析】第一问中主要利用三角函数的两角和差公式化简为单一三角函数解析式
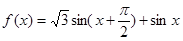 =
=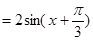
然后利用周期公式得到第一问。
第二问中,由于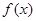 的图象向右平移
的图象向右平移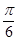 个单位,得到函数
个单位,得到函数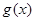 的图象,
的图象,
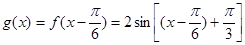
然后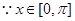 时,
时,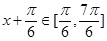 结合三角函数值域求解得到范围。
结合三角函数值域求解得到范围。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com