
题目列表(包括答案和解析)
| e1 |
| e2 |
| a |
| a |
| e1 |
| e2 |
| a |
| i |
| j |
| i |
| j |
| π |
| 3 |
| i |
| j |
| a |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| b |
| a |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| b |
| a |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| A、(1)(2)(3) |
| B、(2)(3)(4) |
| C、(1)(3)(4) |
| D、(1)(2)(4) |
定义平面向量之间的一种运算“*”如下:对任意的 ,令
,令 。给出以下四个命题:(1)若
。给出以下四个命题:(1)若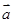 与
与 共线,则
共线,则 ;(2)
;(2)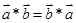 ;(3)对任意的
;(3)对任意的 ,有
,有 ;(4)
;(4) 。
。
(注:这里 指
指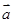 与
与 的数量积)
的数量积)
则其中所有真命题的序号是( )
(A)(1)(2)(3) (B)(2)(3)(4) (C)(1)(3)(4) (D)(1)(2)(4)
 ,令
,令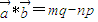 .给出以下四个命题:(1)若
.给出以下四个命题:(1)若 与
与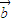 共线,则
共线,则 ;(2)
;(2) ;(3)对任意的λ∈R,有
;(3)对任意的λ∈R,有 ;(4)
;(4) =
= .(注:这里
.(注:这里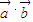 指
指 与
与 的数量积)其中所有真命题的序号是 .
的数量积)其中所有真命题的序号是 .湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com