
题目列表(包括答案和解析)
已知 中,
中, ,
, .设
.设 ,记
,记 .
.
(1) 求 的解析式及定义域;
的解析式及定义域;
(2)设 ,是否存在实数
,是否存在实数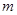 ,使函数
,使函数 的值域为
的值域为 ?若存在,求出
?若存在,求出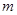 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【解析】第一问利用(1)如图,在 中,由
中,由 ,,
,,
可得 ,
,
又AC=2,故由正弦定理得

(2)中
由 可得
可得

 .显然,
.显然, ,则
,则
1 当m>0的值域为
当m>0的值域为
 m+1=3/2,n=1/2
m+1=3/2,n=1/2
2 当m<0,不满足
当m<0,不满足 的值域为
的值域为 ;
;
因而存在实数m=1/2 的值域为
的值域为 .
.
设定义在(0,+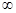 )上的函数
)上的函数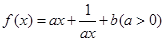
(Ⅰ)求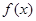 的最小值;
的最小值;
(Ⅱ)若曲线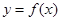 在点
在点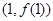 处的切线方程为
处的切线方程为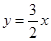 ,求
,求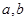 的值。
的值。
【解析】 (Ⅰ)因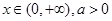 ,故
,故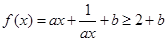 ,取等号的条件是
,取等号的条件是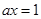 ,即
,即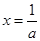 。
。
(Ⅱ)因 ,由
,由 ,求得
,求得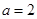 ,又由
,又由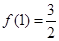 ,可得
,可得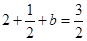 ,解得
,解得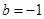
汽车在行驶中,由于惯性作用,刹车后还要继续向前滑行一段距离才能停住,我们称这段距离为“刹车距离”.刹车距离是分析事故的一个重要因素.在一个限速40千米/小时以内的弯道上,甲乙两辆汽车相向而行,发现情况不对,同时刹车,但还是相碰了.事发后,现场测得甲车的刹车距离略超过12米,乙车的刹车距离略超过10米.又知甲、乙两种车型的汽车刹车距离s(米)与车速x(千米/小时)之间分别有如下关系:
s甲=0.1x+0.01x2
s乙=0.05x+0.005x2
问超速行驶应负主要责任的是谁?
s甲=0.1x+0.01x2
s乙=0.05x+0.005x2
问超速行驶应负主要责任的是谁?
A
[解析] ∵a=![]() ,x>0时,x+
,x>0时,x+![]() ≥2
≥2![]() =1,等号在x=
=1,等号在x=![]() 时成立,又a=4时,x+
时成立,又a=4时,x+![]() =x+
=x+![]() ≥2
≥2![]() =4也满足x+
=4也满足x+![]() ≥1,故选A.
≥1,故选A.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com