练习册

  • 练习册
  • 试题
    3．已知cos a ＝cos x·sin g .cos b ＝sin x·sin g .求证sin2 a +sin2 b +sin2 g ＝2 [提示] 利用已知条件.注意到sin2 a ＝1-cos2 a .sin2 b ＝1-cos2 b .将条件代入原式的左边.化简即可． [答案]左边＝1-cos2 a +1-cos2 b +sin2 g ＝2-cos2 a -cos2 b +sin2 g . 又cos a ＝cos x sin g .cos b ＝sin x sin g . ∴ 左边＝2-cos2 x sin2 g -sin2 x sin2 g +sin2 g ＝2-sin2 g(sin2 x+cos2 x)+sin2 g ＝2-sin2 g+sin2 g ＝2 ∴ 原结论成立． [点评] 本题通过三角恒等式的证明.考查三角函数恒等变形能力．寻求已知条件与所证恒等式之间的关系是证明的关键． 【查看更多】

     

    题目列表(包括答案和解析)

    已知函数f(x)＝cos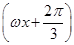 (x∈R，ω>0)的最小正周期为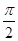，为了得到函数g(x)＝sinωx的图象，只要将y＝f(x)的图象(　　)

    A．向左平移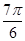个单位长度

    B．向右平移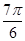个单位长度

    C．向左平移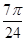个单位长度

    D．向右平移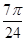个单位长度

     

    查看答案和解析>>

    已知f(x)＝sin(x＋),g(x)＝cos(x－），则f(x)的图象

    A.与g(x)的图象相同

    B.与g(x)的图象关于y轴对称

    C.向左平移个单位，得到g(x)的图象

    D.向右平移个单位，得到g(x)的图象                        

     

    查看答案和解析>>

    已知f(x)＝sin(x＋)，g(x)＝cos(x－)，则下列结论中不正确的是

    A．函数y＝f(x)g(x)的最小正周期为π           B．函数y＝f(x)g(x)的最大值为

    C．函数y＝f(x)g(x)的图象关于点(，0)成中心对称  D．函数y＝f(x)g(x)是奇函数

     

    查看答案和解析>>

    已知f(x)＝sin(x＋)，g(x)＝cos(x－)，则下列结论中不正确的是
    A．函数y＝f(x)g(x)的最小正周期为π
    B．函数y＝f(x)g(x)的最大值为
    C．函数y＝f(x)g(x)的图象关于点(，0)成中心对称
    D．函数y＝f(x)g(x)是奇函数

    查看答案和解析>>

    向量a＝(sinωx＋cosωx，1)，b＝(f(x)，simωx)，其中0＜ω＜l，且a∥b．将f(x)的图象沿x轴向左平移个单位，沿y轴向下平移个单位，得到g(x)的图象，已知g(x)的图象关于(，0)对称

    (1)求ω的值；

    (2)求g(x)在[0，4π]上的单调递增区间．

    查看答案和解析>>


    同步练习册答案