题目列表(包括答案和解析)
设函数y＝sin(ωx＋φ)＋1(ω>0)的一段图象如右图所示，则周期T、初相φ的值依次为( )
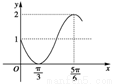
A．π，－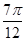
B．2π，
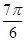
C．π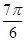，－ D．2π，－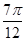
设函数f(θ)＝
sinθ＋cosθ，其中，角θ的顶点与坐标原点重合，始边与x轴非负半轴重合，终边经过点P(x，y)，且0≤θ≤π.
(1)若点P的坐标为
，求f(θ)的值；
(2)若点P(x，y)为平面区域Ω：
，上的一个动点，试确定角θ的取值范围，并求函数f(θ)的最小值和最大值．
下列命题：
①函数y＝sin(x－
)在[0，π]上是减函数；②点A(1,1)、B(2,7)在直线3x－y＝0两侧；③数列{an}为递减的等差数列，a1＋a5＝0，设数列{an}的前n项和为Sn，则当n＝4时，Sn取得最大值；
④定义运算
＝a1b2－a2b1，则函数f(x)＝
的图像在点(1，
)处的切线方程是6x－3y－5＝0.其中正确命题的序号是________．(把所有正确命题的序号都写上)．
有下列命题：
①命题“
x∈R，使得x2＋1＞3x”的否定是“
x∈R，都有x2＋1≤3x”；
②设p、q为简单命题，若“p∨q”为假命题，则“
p∧q为真命题”；
③“a＞2”是“a＞5”的必要条件；
④若函数f(x)＝(x＋1)(x＋a)为偶函数，则a＝－1；
⑤将函数y＝sin(2x)(x∈R)的图像向右平移
个单位即可得到函数y＝sin(2x－
)(x∈R)的图像；其中所有正确的说法序号是________．
设棕＞0，函数y＝sin(棕x＋
)＋2的图像向右平移
个单位后与原图像重合，则棕的最小值是
3
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com