题目列表(包括答案和解析)
求证：(1)tanα＋secα＝
；
(2)tan2α＋cot2α＋1＝(tan2α＋tanα＋1)(cot2α－cotα＋1)．
(14分)已知tanα＝
，求证：
(1)
=－
；
(2)sin2α＋sinαcosα＝
．
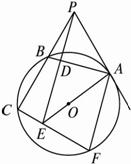
图2-5-6
（1）求证:△PBD∽△PEC;
（2）若AB＝12,tan∠EAF＝
,求⊙O的半径.
如图，已知ABCD－A1B1C1D1是棱长为3的正方体，点E在AA1上，点F在CC1上，且AE＝FC1＝1.
(1)求证：E，B，F，D1四点共面；
(2)若点G在BC上，BG＝
，点M在BB1上，GM⊥BF，垂足为H，求证：
EM⊥平面BCC1B1；
(3)用θ表示截面EBFD1和侧面BCC1B1所成的锐二面角的大小，求tanθ.
已知椭圆
＋
＝1与双曲线
－
＝1有相同的焦点，P是它们的公共点，设∠F1PF2＝2α，求证：tanα＝
．(如图)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com