
题目列表(包括答案和解析)
下列命题是真命题的是:①![]() 存在唯一的实数
存在唯一的实数![]() ,使
,使![]()
![]()
![]() ;②
;②![]() 存在不全为零的实数
存在不全为零的实数![]() ,使
,使![]()
![]()
![]()
![]() ;③
;③![]() 与
与![]() 不共线
不共线![]() 若存在实数
若存在实数![]() ,使
,使![]()
![]()
![]()
![]() ,则
,则![]() ;④
;④![]() 与
与![]() 不共线
不共线![]() 不存在实数
不存在实数![]() 使
使![]()
![]()
![]() .
.
A.①和③ B.②和③ C.①和② D. ③和④
| a |
| b |
| b |
| c |
| a |
| c |
| a |
| b |
| c |
| a |
| b |
| b |
| a |
| OM |
| 1 |
| 3 |
| OA |
| 1 |
| 3 |
| OB |
| 1 |
| 3 |
| OC |
下列命题:
①若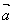 与
与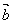 共线,
共线, 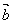 与
与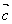 共线,则
共线,则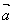 与
与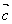 共线;
共线;
②向量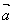 、
、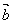 、
、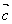 共面,则它们所在直线也共面;
共面,则它们所在直线也共面;
③若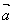 与
与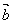 共线,则存在唯一的实数
共线,则存在唯一的实数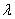 ,使
,使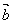 =
=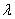
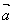 ;
;
④若A、B、C三点不共线,0是平面ABC外一点.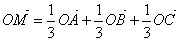 ,则点M一定在平面ABC上,且在△ABC内部,
,则点M一定在平面ABC上,且在△ABC内部,
上述命题中的真命题是 .
若存在实常数 和
和 ,使得函数
,使得函数 和
和 对其公共定义域上的任意实数
对其公共定义域上的任意实数 都满足:
都满足: 和
和 恒成立,则称此直线
恒成立,则称此直线 为
为 和
和 的“隔离直线”.已知函数
的“隔离直线”.已知函数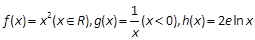 .有下列命题:
.有下列命题:
① 在
在 内单调递增;
内单调递增;
② 和
和 之间存在“隔离直线”, 且b的最小值为-4;
之间存在“隔离直线”, 且b的最小值为-4;
③ 和
和 之间存在“隔离直线”, 且k的取值范围是
之间存在“隔离直线”, 且k的取值范围是 ;
;
④ 和
和 之间存在唯一的“隔离直线”
之间存在唯一的“隔离直线” .
.
其中真命题的个数有( ).
| A.1个 | B.2个 | C.3个 | D.4个 |
 和
和 ,使得函数
,使得函数 和
和 对其公共定义域上的任意实数
对其公共定义域上的任意实数 都满足:
都满足: 和
和 恒成立,则称此直线
恒成立,则称此直线 为
为 和
和 的“隔离直线”.已知函数
的“隔离直线”.已知函数 .有下列命题:
.有下列命题: 在
在 内单调递增;
内单调递增; 和
和 之间存在“隔离直线”, 且b的最小值为-4;
之间存在“隔离直线”, 且b的最小值为-4; 和
和 之间存在“隔离直线”, 且k的取值范围是
之间存在“隔离直线”, 且k的取值范围是 ;
; 和
和 之间存在唯一的“隔离直线”
之间存在唯一的“隔离直线” .
.| A.1个 | B.2个 | C.3个 | D.4个 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com