练习册

  • 练习册
  • 试题
    6． 结合的图象观察参数的变化对函数图象的影响,能应用三角函数解决一些简单的实际问题. [例题分析] 【查看更多】

     

    题目列表(包括答案和解析)

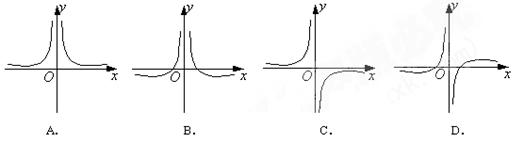
    　函数的图象大致是（　　　　）

     

     

    查看答案和解析>>

    将函数图象向右平移个单位后，

    　　得到的图象，若函数的图象和的图象关于x轴对称，求.

     

    查看答案和解析>>

    下列四个命题：
    　　　　①函数的值域是(-∞，-2]∪[2，+∞)；
    　　　　②命题与命题，若是的充分不必要条件，则是的充分不必要条件；
    　　　　③函数的图象经过第一象限；
    　　　　④函数的反函数是；
    　　　　其中正确命题的序号是____________。（把你认为正确的序号都填上）。

    查看答案和解析>>

    将函数图象向右平移个单位后，

    　　得到的图象，若函数的图象和的图象关于x轴对称，求.

     

    查看答案和解析>>

    设y=f（x）是某港口水的深度y（米）关于时间t（时）的函数，其中0≤t≤24，下表是该港口某一天从0时至24时记录的时间t与水深y的关系：
    t 0 3 6 9 12 15 18 21 24
    y 12 15.1 12.1 9.1 11.9 14.9 11.9 8.9 12.1
    经长期观察，函数y=f（t）的图象可以近似地看成函数y=k+Asin（ωt+φ）的图象，下面的函数中，最能近似表示表中数据间对应关系的函数是（t∈[0，24]）（　　）

    查看答案和解析>>


    同步练习册答案