
题目列表(包括答案和解析)

 (2013•朝阳区一模)国家环境标准制定的空气质量指数与空气质量等级对应关系如下表:
(2013•朝阳区一模)国家环境标准制定的空气质量指数与空气质量等级对应关系如下表:| 空气质量指数 | 0-50 | 51-100 | 101-150 | 151-200 | 201-300 | 300以上 |
| 空气质量等级 | 1级优 | 2级良 | 3级轻度污染 | 4级中度污染 | 5级重度污染 | 6级严重污染 |
| 1 |
| n |
. |
| x |
. |
| x |
. |
| x |
. |
| x |
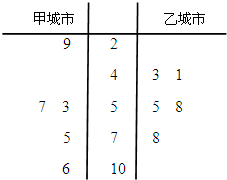
 (2013•德州二模)为了解某校教师使用多媒体进行教学的情况,将全校200名 教师按一学期使用多媒体进行教学的次数分成了[0,9),[10,19),[20,29),[30,39),[40,49)五层.现采用分层抽样从该校教师中抽取20名教师,调查了他们上学期使用多媒体进行教学的次数,结果用茎叶图表示如图,据此可知该校一学期使用多媒体进行教学的次数在[30,39)内的教师人数为
(2013•德州二模)为了解某校教师使用多媒体进行教学的情况,将全校200名 教师按一学期使用多媒体进行教学的次数分成了[0,9),[10,19),[20,29),[30,39),[40,49)五层.现采用分层抽样从该校教师中抽取20名教师,调查了他们上学期使用多媒体进行教学的次数,结果用茎叶图表示如图,据此可知该校一学期使用多媒体进行教学的次数在[30,39)内的教师人数为湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com