
题目列表(包括答案和解析)
【解析】如图:|OB|=b,|O F1|=c.∴kPQ=![]() ,kMN=﹣
,kMN=﹣![]() .
.
直线PQ为:y=![]() (x+c),两条渐近线为:y=
(x+c),两条渐近线为:y=![]() x.由
x.由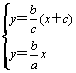 ,得:Q(
,得:Q(![]() ,
,![]() );由
);由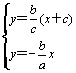 ,得:P(
,得:P(![]() ,
,![]() ).∴直线MN为:y-
).∴直线MN为:y-![]() =﹣
=﹣![]() (x-
(x-![]() ),
),
令y=0得:xM=![]() .又∵|MF2|=|F1F2|=2c,∴3c=xM=
.又∵|MF2|=|F1F2|=2c,∴3c=xM=![]() ,解之得:
,解之得:![]() ,即e=
,即e=![]() .
.
【答案】B
已知数列 中,
中, ,
, ,数列
,数列 中,
中, ,且点
,且点 在直线
在直线 上。
上。
(1)求数列 的通项公式;
的通项公式;
(2)求数列 的前
的前 项和
项和 ;
;
(3)若 ,求数列
,求数列 的前
的前 项和
项和 ;
;
【解析】第一问中利用数列的递推关系式
 ,因此得到数列
,因此得到数列 的通项公式;
的通项公式;
第二问中, 在
在 即为:
即为:
即数列 是以
是以 的等差数列
的等差数列
得到其前n项和。
第三问中, 又
又 

 ,利用错位相减法得到。
,利用错位相减法得到。
解:(1)
 即数列
即数列 是以
是以 为首项,2为公比的等比数列
为首项,2为公比的等比数列

 ……4分
……4分
(2) 在
在 即为:
即为:
即数列 是以
是以 的等差数列
的等差数列

 ……8分
……8分
(3) 又
又 


 ①
①  ②
②
①- ②得到


|
| A、4 | B、2 | C、5 | D、25 |
先阅读理解下面的例题,再按要求解答:
例题:解一元二次不等式![]() .
.
解:∵![]() ,
,
∴![]() .
.
由有理数的乘法法则“两数相乘,同号得正”,有
(1)![]() (2)
(2)![]()
解不等式组(1),得![]() ,
,
解不等式组(2),得![]() ,
,
故![]() 的解集为
的解集为![]() 或
或![]() ,
,
即一元二次不等式![]() 的解集为
的解集为![]() 或
或![]() .
.
问题:求分式不等式![]() 的解集.
的解集.
先阅读理解下面的例题,再按要求解答:
例题:解一元二次不等式![]() .
.
解:∵![]() ,
,
∴![]() .
.
由有理数的乘法法则“两数相乘,同号得正”,有
(1)![]() (2)
(2)![]()
解不等式组(1),得![]() ,
,
解不等式组(2),得![]() ,w.w.w.k.s.5.u.c.o.m
,w.w.w.k.s.5.u.c.o.m ![]()
![]()
故![]() 的解集为
的解集为![]() 或
或![]() ,
,
即一元二次不等式![]() 的解集为
的解集为![]() 或
或![]() .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com