
题目列表(包括答案和解析)
(本题12分)研究人员发现某种特别物质的温度y(单位:摄氏度)随时间x(单位:分钟)的变化规律是:![]() 。
。
(1)如果![]() ,求经过多少时间,温度为5摄氏度;
,求经过多少时间,温度为5摄氏度;
(2)若该物质的温度总不低于2摄氏度,求![]() 的取值范围。
的取值范围。
(本题满分12分)探究函数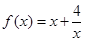 ,
,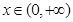 的最小值,并确定取得最小值时
的最小值,并确定取得最小值时 的值,列表如下:
的值,列表如下:
|
|
… |
0.5 |
1 |
1.5 |
1.7 |
1.9 |
2 |
2.1 |
2.2 |
2.3 |
3 |
4 |
5 |
7 |
… |
|
|
… |
8.5 |
5 |
4.17 |
4.05 |
4.005 |
4 |
4.005 |
4.102 |
4.24 |
4.3 |
5 |
5.8 |
7.57 |
… |
请观察表中 值随
值随 值变化的特点,完成下列问题:
值变化的特点,完成下列问题:
(1) 当 时,
时,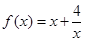 在区间
在区间 上递减,在区间 上递增;
上递减,在区间 上递增;
所以, =
时,
=
时,  取到最小值为
;
取到最小值为
;
(2) 由此可推断,当 时,
时,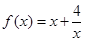 有最
值为 ,此时
有最
值为 ,此时 =
;
=
;
(3) 证明: 函数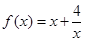 在区间
在区间 上递减;
上递减;
(4) 若方程 在
在 内有两个不相等的实数根,求实数
内有两个不相等的实数根,求实数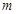 的取值范围。
的取值范围。
(本题满分12分)已知椭圆C: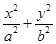 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,以原点为圆点,椭圆的短半轴为半径的圆与直线x-y+
,以原点为圆点,椭圆的短半轴为半径的圆与直线x-y+ =0相切。
=0相切。
(Ⅰ)求椭圆的标准方程;
(Ⅱ)设P(4,0),A,B是椭圆C上关于x轴对称的任意两个不同的点,连接PB交随圆C于另一点E,证明直线AE与x轴相交于定点Q.
(本题满分12分)探究函数 的最小值,并确定取得最小值时x的值. 列表如下, 请观察表中y值随x值变化的特点,完成以下的问题.
的最小值,并确定取得最小值时x的值. 列表如下, 请观察表中y值随x值变化的特点,完成以下的问题.
|
x |
… |
0.25 |
0.5 |
0.75 |
1 |
1.1 |
1.2 |
1.5 |
2 |
3 |
5 |
… |
|
y |
… |
8.063 |
4.25 |
3.229 |
3 |
3.028 |
3.081 |
3.583 |
5 |
9.667 |
25.4 |
… |
已知:函数 在区间(0,1)上递减,问:
在区间(0,1)上递减,问:
(1)函数 在区间
上递增.当
在区间
上递增.当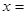 时,
时,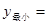 ;
;
(2)函数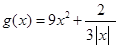 在定义域内有最大值或最小值吗?如有,是多少?此时x为何值?(直接回答结果,不需证明)
在定义域内有最大值或最小值吗?如有,是多少?此时x为何值?(直接回答结果,不需证明)
(本题满分12分)探究函数![]() ,
,![]() 的最小值,并确定取得最小值时
的最小值,并确定取得最小值时![]() 的值,列表如下:
的值,列表如下:
|
| … | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | … |
|
| … | 8.5 | 5 | 4.17 | 4.05 | 4.005 | 4 | 4.005 | 4.102 | 4.24 | 4.3 | 5 | 5.8 | 7.57 | … |
请观察表中![]() 值随
值随![]() 值变化的特点,完成下列问题:
值变化的特点,完成下列问题:
(1) 当![]() 时,
时,![]() 在区间
在区间![]() 上递减,在区间 上递增;
上递减,在区间 上递增;
所以,![]() = 时,
= 时, ![]() 取到最小值为 ;
取到最小值为 ;
(2) 由此可推断,当![]() 时,
时,![]() 有最 值为 ,此时
有最 值为 ,此时![]() = ;
= ;
(3) 证明: 函数![]() 在区间
在区间![]() 上递减;
上递减;
(4) 若方程![]() 在
在![]() 内有两个不相等的实数根,求实数
内有两个不相等的实数根,求实数![]() 的取值范围。
的取值范围。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com