
题目列表(包括答案和解析)
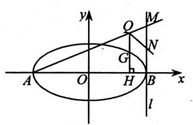 已知椭圆C:
已知椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| 2 |
| MF |
| MF′| |
| 2 |
如图,已知椭圆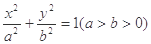 的长轴为AB,过点B的直线
的长轴为AB,过点B的直线 与
与
轴垂直,椭圆的离心率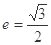 ,F为椭圆的左焦点,且
,F为椭圆的左焦点,且
(1)求此椭圆的标准方程;
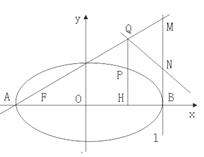
(2)设P是此椭圆上异于A,B的任意一点,  轴,H为垂足,延长HP到点Q,使得HP=PQ,连接AQ并延长交直线
轴,H为垂足,延长HP到点Q,使得HP=PQ,连接AQ并延长交直线 于点
于点 ,
, 为
为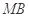 的中点,判定直线
的中点,判定直线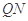 与以
与以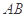 为直径的圆O位置关系。
为直径的圆O位置关系。
 .
.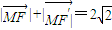 .
.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com