
题目列表(包括答案和解析)
某同学在一次研究性学习中发现,以下五个式子的值都等于同一个常数 .
.
① ;
;
② ;
;
③ ;
;
④ ;
;
⑤ .
.
(1)从上述五个式子中选择一个,求出常数 ;
;
(2)根据(1)的计算结果,将该同学的发现推广为一个三角恒等式,并证明你的结论.
某同学在一次研究性学习中发现,以下五个式子的值都等于同一个常数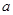 .
.
①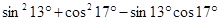 ;
;
②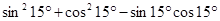 ;
;
③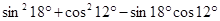 ;
;
④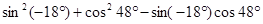 ;
;
⑤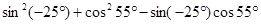 .
.
(1)从上述五个式子中选择一个,求出常数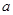 ;
;
(2)根据(1)的计算结果,将该同学的发现推广为一个三角恒等式,并证明你的结论.
某同学在一次研究性学习中发现,以下五个式子的值都等于同一个常数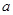 .
.
① ;
;
② ;
;
③ ;
;
④ ;
;
⑤ .
.
(1)从上述五个式子中选择一个,求出常数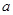 ;
;
(2)根据(1)的计算结果,将该同学的发现推广为一个三角恒等式,并证明你的结论.
某同学在一次研究性学习中发现,以下五个式子的值都等于同一个常数 .
.
① ;
;
② ;
;
③ ;
;
④ ;
;
⑤ .
.
(1)从上述五个式子中选择一个,求出常数 ;
;
(2)根据(1)的计算结果,将该同学的发现推广为一个三角恒等式,并证明你的结论.
(2012年高考(福建文))某同学在一次研究性学习中发现,以下五个式子的值都等于同一个常数.
(1)![]()
(2)![]()
(3)![]()
(4)![]()
(5)![]()
Ⅰ 试从上述五个式子中选择一个,求出这个常数
Ⅱ 根据(Ⅰ)的计算结果,将该同学的发现推广为三角恒等式,并证明你的结论.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com