
题目列表(包括答案和解析)
解关于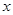 的不等式:
的不等式:

【解析】解:当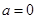 时,原不等式可变为
时,原不等式可变为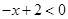 ,即
,即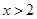 (2分)
(2分)
当 时,原不等式可变为
时,原不等式可变为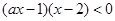
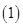 (5分) 若
(5分) 若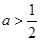 时,
时,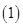 的解为
的解为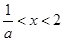 (7分)
(7分)
若 时,
时,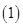 的解为
的解为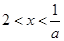 (9分) 若
(9分) 若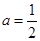 时,
时,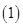 无解(10分) 若
无解(10分) 若 时,
时,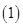 的解为
的解为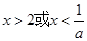 (12分综上所述
(12分综上所述
当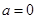 时,原不等式的解为
时,原不等式的解为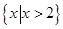
当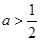 时,原不等式的解为
时,原不等式的解为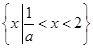
当 时,原不等式的解为
时,原不等式的解为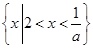
当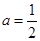 时,原不等式的解为
时,原不等式的解为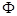
当 时,原不等式的解为:
时,原不等式的解为: 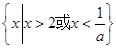
纠正以下解题过程的错误:
题:若|ab|+1=|a|+|b|,a,b为实数,求a,b.
解:原式可化为(|a|-1)(|b|-1)=0,
∴|a|=1,|b|=1,①
∴a=±1,b=±1,②
纠正①________;②________
| 2 |
| 2 |
| A.1 | B.2 | C.3 | D.4 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com