（理科做）
阅读下面题目的解法，再根据要求解决后面的问题．
阅读题目：对于任意实数a
1，a
2，b
1，b
2，证明不等式（a
1b
1+a
2b
2）
2≤（a
12+a
22）（b
12+b
22）．
证明：构造函数f（x）=（a
1x+b
1）
2+（a
2x+b
2）
2=（a
12+a
22）x
2+2（a
1b
1+a
2b
2）x+（b
12+b
22）．
注意到f（x）≥0，所以△=[2（a
1b
1+a
2b
2）]
2-4（a
12+a
22）（b
12+b
22）≤0，
即（a
1b
1+a
2b
2）
2≤（a
12+a
22）（b
12+b
22）．
（其中等号成立当且仅当a
1x+b
1=a
2x+b
2=0，即a
1b
2=a
2b
1．）
问题：（1）请用这个不等式证明：对任意正实数a，b，x，y，不等式
+≥成立．
（2）用（1）中的不等式求函数
y=+(0＜x＜)的最小值，并指出此时x的值．
（3）根据阅读题目的证明，将不等式（a
1b
1+a
2b
2）
2≤（a
12+a
22）（b
12+b
22）进行推广，得到一个更一般的不等式，并用构造函数的方法对你的推广进行证明．
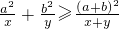成立．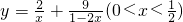
的最小值，并指出此时x的值．