A.

【命题意图】本题考查导数的概念与几何意义，中等题.

已知函数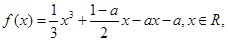其中a>0.

（I）求函数f(x)的单调区间；

（II）若函数f（x）在区间（-2，0）内恰有两个零点，求a的取值范围；

（III）当a=1时，设函数f（x）在区间[t,t+3]上的最大值为M（t），最小值为m（t）,记g(t)=M(t)-m(t),求函数g(t)在区间[-3，-1]上的最小值。

【考点定位】本小题主要考查导数的运算，利用导数研究函数的单调性、函数的零点，函数的最值等基础知识.考查函数思想、分类讨论思想.考查综合分析和解决问题的能力.

已知抛物线C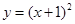：与圆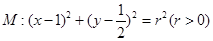有一个公共点A，且在A处两曲线的切线与同一直线l

（I）     求r；

（II）   设m、n是异于l且与C及M都相切的两条直线，m、n的交点为D，求D到l的距离。

【解析】本试题考查了抛物线与圆的方程，以及两个曲线的公共点处的切线的运用，并在此基础上求解点到直线的距离。

【点评】该试题出题的角度不同于平常，因为涉及的是两个二次曲线的交点问题，并且要研究两曲线在公共点出的切线，把解析几何和导数的工具性结合起来，是该试题的创新处。另外对于在第二问中更是难度加大了，出现了另外的两条公共的切线，这样的问题对于我们以后的学习也是一个需要练习的方向。

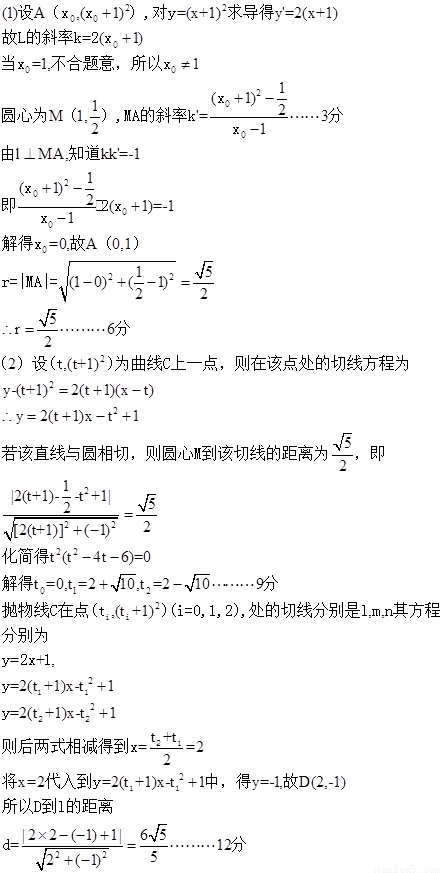
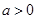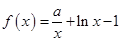已知，函数（其中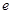为自然对数的底数）．

  （Ⅰ）求函数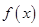在区间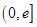上的最小值；

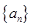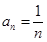  （Ⅱ）设数列的通项，是前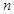项和，证明：．

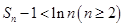【解析】本试题主要考查导数在研究函数中的运用，求解函数给定区间的最值问题，以及能结合数列的相关知识，表示数列的前n项和，同时能构造函数证明不等式的数学思想。是一道很有挑战性的试题。

已知函数f(x)＝alnx＋bx,且f(1)＝ －1，f′(1)＝0，

⑴求f(x)；

⑵求f(x)的最大值；

⑶若x＞0,y＞0,证明：lnx＋lny≤.

本题主要考查函数、导数的基本知识、函数性质的处理以及不等式的综合问题，同时考查考生用函数放缩的方法证明不等式的能力．