
题目列表(包括答案和解析)
| a |
| a |
下面给出了关于复数的四种类比推理:
①复数的加减法运算可以类比多项式的加减法运算法则;
②由向量 的性质
的性质 类比得到复数
类比得到复数 的性质
的性质 ;
;
③方程 有两个不同实数根的条件是
有两个不同实数根的条件是 可以类比得到:方程
可以类比得到:方程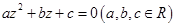 有两个不同复数根的条件是
有两个不同复数根的条件是 ;
;
④由向量加法的几何意义可以类比得到复数加法的几何意义
其中类比得到的结论错误的是
A.①③ B.②④ C.②③ D.①④
下面给出了关于复数的四种类比推理:
① 复数的加减法运算法则,可以类比多项式的加减法运算法则;
② 由向量  的性质
的性质  ,可以类比得到复数
,可以类比得到复数
 的性质
的性质  ;
;
③ 方程  (a 、b 、c ∈ R )有两个不同实根的条件是
(a 、b 、c ∈ R )有两个不同实根的条件是 , 类比可以得到 方程
, 类比可以得到 方程  (a 、b 、c ∈ C)有两个不同复数根的条件是
(a 、b 、c ∈ C)有两个不同复数根的条件是  ;
;
④ 由向量加法的几何意义,可以类比得到复数加法的几何意义.
其中类比得到的结论正确的是( )
A、① ③ B、 ② ④ C、② ③ D、① ④
下面给出了关于复数的四种类比推理:
① 复数的加减法运算,可以类比多项式的加减法运算法则;
② 由向量  的性质
的性质
 ,可以类比得到复数
,可以类比得到复数  的性质
的性质
 ;
;
③ 方程  (a 、b 、c ∈ R )有两个不同实根的条件是
(a 、b 、c ∈ R )有两个不同实根的条件是 ,类比可以得到
方程
,类比可以得到
方程 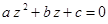 (a 、b 、c ∈ C)有两个不同复数根的条件是
(a 、b 、c ∈ C)有两个不同复数根的条件是
 ;
;
④ 由向量加法的几何意义,可以类比得到复数加法的几何意义。
其中类比得到的结论正确的是( *** )
A.① ③ B..② ④ C.② ③ D.① ④
下面给出了关于复数的四种类比推理:
①复数的加减法运算可以类比多项式的加减法运算法则;
②由向量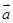 的性质
的性质 类比得到复数
类比得到复数 的性质
的性质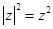 ;
;
③方程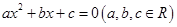 有两个不同实数根的条件是
有两个不同实数根的条件是 可以类比得到:方程
可以类比得到:方程 有两个不同复数根的条件是
有两个不同复数根的条件是 ;
;
④由向量加法的几何意义可以类比得到复数加法的几何意义
其中类比得到的结论错误的是
| A.①③ | B.②④ | C.②③ | D.①④ |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com