
题目列表(包括答案和解析)
 ,则实数k的值为( )。
,则实数k的值为( )。 A,至少存在一个i∈{1,2,3,…,m},使Ai∩{x,y}={x}或{y};
A,至少存在一个i∈{1,2,3,…,m},使Ai∩{x,y}={x}或{y}; ,
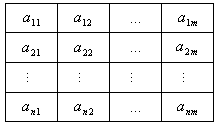
,
 ,若
,若 ,则实数k的值为( )。
,则实数k的值为( )。 ,则f(0)+f(1)=( ),若Sk-1=
,则f(0)+f(1)=( ),若Sk-1= (k≥2,k∈N*),则Sk-1=( )(用含有k的代数式表示)。
(k≥2,k∈N*),则Sk-1=( )(用含有k的代数式表示)。  ,若
,若 ,则实数k的取值为 ▲ 。
,则实数k的取值为 ▲ 。湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com