
题目列表(包括答案和解析)
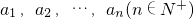 ,任意选取一个实数c,变换T(c)将数列a1,a2,…,an变换为数列|a1-c|,|a2-c|,…,|an-c|,再将得到的数列继续实施这样的变换,这样的变换可以连续进行多次,并且每次所选择的实数c可以不相同,第k(k∈N+)次变换记为Tk(ck),其中ck为第k次变换时选择的实数.如果通过k次变换后,数列中的各项均为0,则称T1(c1),T2(c2),…,Tk(ck)为“k次归零变换”
,任意选取一个实数c,变换T(c)将数列a1,a2,…,an变换为数列|a1-c|,|a2-c|,…,|an-c|,再将得到的数列继续实施这样的变换,这样的变换可以连续进行多次,并且每次所选择的实数c可以不相同,第k(k∈N+)次变换记为Tk(ck),其中ck为第k次变换时选择的实数.如果通过k次变换后,数列中的各项均为0,则称T1(c1),T2(c2),…,Tk(ck)为“k次归零变换”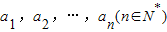 ,任意选取一个实数c,变换T(c)将数列a1,a2,…,an变换为数列|a1-c|,|a2-c|,…,|an-c|,再将得到的数列继续实施这样的变换,这样的变换可以连续进行多次,并且每次所选择的实数c可以不相同,第k(k∈N*)次变换记为Tk(ck),其中ck为第k次变换时选择的实数.如果通过k次变换后,数列中的各项均为0,则称T1(c1),T2(c2),…,Tk(ck)为“k次归零变换”
,任意选取一个实数c,变换T(c)将数列a1,a2,…,an变换为数列|a1-c|,|a2-c|,…,|an-c|,再将得到的数列继续实施这样的变换,这样的变换可以连续进行多次,并且每次所选择的实数c可以不相同,第k(k∈N*)次变换记为Tk(ck),其中ck为第k次变换时选择的实数.如果通过k次变换后,数列中的各项均为0,则称T1(c1),T2(c2),…,Tk(ck)为“k次归零变换”| 3 |
| 2 |
| 1 |
| 1+3l |
| 1 |
| 1+3k |
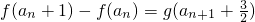 .数列{bn}满足
.数列{bn}满足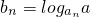 ,设
,设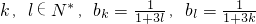 .
.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com