
题目列表(包括答案和解析)
9. =( ).
=( ).
A.1; B.2; C.3 D.4.
8.由直线与圆相切时,圆心与切点连线与直线垂直,想到平面与球相切时,球心与切点连线与平面垂直,用的是( )
A归纳推理 B演绎推理 C类比推理 D特殊推理
7.在 的展开式中,含
的展开式中,含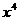 的项的系数是( )
的项的系数是( )
A.-15 B.85 C.-120 D.274
6.三张卡片的正反面上分别写有数字0与2,3与4,5与6,把这三张卡片拼在一起表示一个三位数,则三位数的个数为 ( )
A. 36 B.40 C.44 D.48
5.12名同学分别到三个不同的路口进行车流量的调查,若每个路口4人,则不同的分配
方案共有( )
A. B.
B.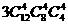 C.
C.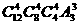 D.
D.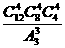
4.下列求导运算正确的是( )
A.(x+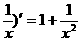 B.(log2x)′=
B.(log2x)′=
C.(3x)′=3xlog3e D.(x2cosx)′=-2xsinx
3.曲线 在点
在点 处的切线的倾斜角为( )
处的切线的倾斜角为( )
A.30° B.45° C.60° D.120°
2.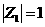 ,
,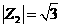 ,
, ,则
,则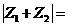 ( )
( )
A. B.
B.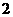 C.
C.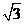 D.
D.
1. 的值是( ).
的值是( ).
A. B.
B. C.
C. D.
D.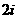
18. 解  ⑴
⑴  …………1分
…………1分
由题意知,1与3是方程 的两根, …………2分
的两根, …………2分
于是 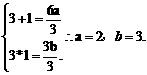 …………4分
…………4分

当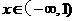 时,
时, 当
当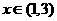 时,
时, 当
当 时,
时,
故当x (
( , 1)时,f(x)是增函数,当 x
, 1)时,f(x)是增函数,当 x (3,
(3, )时,f(x)也是增函数,
)时,f(x)也是增函数,
但当x (1 ,3)时,f(x)是减函数. ……………………………7分
(1 ,3)时,f(x)是减函数. ……………………………7分
⑵

当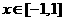 时,
时, 当
当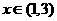 时,
时, 当
当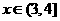 时,
时,
 当
当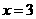 时,
时, 有极小值10c…………9分
有极小值10c…………9分
又 时,
时,  的最小值为10c-16…………10分
的最小值为10c-16…………10分
对任意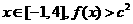 恒成立
恒成立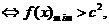 …………11分
…………11分
即
 c的取值范围是
c的取值范围是 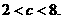 ……………………………13分
……………………………13分
19解:(I)当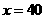 时,汽车从甲地到乙地行驶了
时,汽车从甲地到乙地行驶了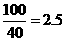 小时,…………2分
小时,…………2分
要耗没 (升)。…………4分
(升)。…………4分
答:当汽车以40千米/小时的速度匀速行驶时,从甲地到乙地耗油17.5升。…………5分
(II)当速度为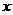 千米/小时时,汽车从甲地到乙地行驶了
千米/小时时,汽车从甲地到乙地行驶了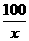 小时,…………6分,设耗油量为
小时,…………6分,设耗油量为 升,依题意得
升,依题意得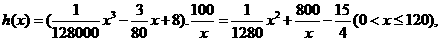 …………8分
…………8分
 令
令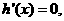 得
得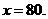 …………10分
…………10分
当 时,
时,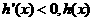 是减函数; 当
是减函数; 当 时,
时,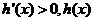 是增函数。
是增函数。
 当
当 时,
时, 取到极小值
取到极小值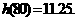
因为 在
在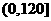 上只有一个极值,所以它是最小值。…………12分
上只有一个极值,所以它是最小值。…………12分
答:当汽车以80千米/小时的速度匀速行驶时,从甲地到乙地耗油最少,最少为11.25升。………13分
20解:(1) ……………………………………2分
……………………………………2分
因为当 时,
时, ,所以
,所以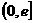 是函数的递增区间;
是函数的递增区间;
当 时,
时, ,所以
,所以 是函数的递减区间;…………5分
是函数的递减区间;…………5分
显然,当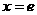 时,函数
时,函数 有最大值,最大值为
有最大值,最大值为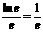 ………………7分。
………………7分。
(2)令 则
则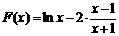 ,
,
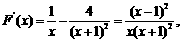 ………………………………………………10分
………………………………………………10分
当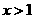 时,
时, ,所以
,所以 在(1,+∞)上为增函数。………………………12分
在(1,+∞)上为增函数。………………………12分
所以当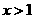 时,
时,  ,………………………13分
,………………………13分
故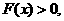 即
即 ………………………………………………14分
………………………………………………14分
21解:(1)令F(x)=f(x)-g(x)=x3+(2-a)x2+4,
∴f(x)≥g(x)在[0,+∞)上恒成立等价于F(x)min≥0(x∈[0,+∞)). ………………………1分
F′(x)= 3x2+2(2-a)x,
①若2-a≥0,即a≤2时,  F(x)在[0,+∞)是增函数,F(x)min=4>0; ………3分
F(x)在[0,+∞)是增函数,F(x)min=4>0; ………3分
②若2-a<0,即a>2时,F′(x)=3x2-2(a-2)x=3x[x-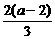 ].由于F′(
].由于F′(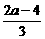 )=0,
)=0,
且当x>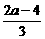 时,F′(x)>0;当0≤x<
时,F′(x)>0;当0≤x<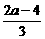 时,F(x)min=F(
时,F(x)min=F(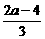 )≥0, ………………………6分
)≥0, ………………………6分
即(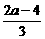 )3-(a-2)(
)3-(a-2)(
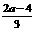 )2+4≥0,得a≤5.∴2<a≤5.又a≤2, ………………………7分
)2+4≥0,得a≤5.∴2<a≤5.又a≤2, ………………………7分
取并集得a的取值范围是(-∞,5]. ………………………8分
(2)由题意f(x)min≥g(x)max,x∈[0,+∞).
x∈[0,+∞)时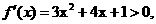 显然,f(x)min=-4(当x=0时,取最小值). ………………10分
显然,f(x)min=-4(当x=0时,取最小值). ………………10分
∵a≥0时,g(x)图像开口向上,无最大值,不合题意, ………………………11分
∴a<0.又∵-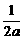 ∈[0,+∞),g(x)max=-
∈[0,+∞),g(x)max=-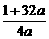 , ………………………13分
, ………………………13分
∴-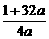 ≤-4.∴a≤-
≤-4.∴a≤- .∴a的取值范围是(-∞,-
.∴a的取值范围是(-∞,- ]. ………………………14分
]. ………………………14分
本资料由《七彩教育网》 提供!
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com