
题目列表(包括答案和解析)
1. 设集合A={4,5,7,9},B={3,4,7,8,9},全集 =A
=A B,则集合
B,则集合 (A
(A B)中的元素共有
( )
B)中的元素共有
( )
A. 3个 B. 4个 C. 5个 D. 6个
22. (本小题满分14分) 已知点Q位于直线 右侧,且到点
右侧,且到点 与到直线
与到直线 的距离之和等于4.
的距离之和等于4.
(1) 求动点Q的轨迹C;
(2)直线 过点
过点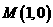 交曲线C于A、B两点,点P满足
交曲线C于A、B两点,点P满足 ,
,
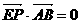 ,又
,又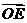 =(
=(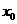 ,0),其中O为坐标原点,求
,0),其中O为坐标原点,求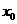 的取值范围;
的取值范围;
(3)在(Ⅱ)的条件下, 能否成为以EF为底的等腰三角形?若能,求出此时直线
能否成为以EF为底的等腰三角形?若能,求出此时直线 的方程;若不能,请说明理由.
的方程;若不能,请说明理由.
20.(本小题满分12分)过点A(-2,4)引倾斜角为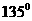 的直线,交曲线为
的直线,交曲线为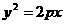
(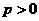 )于
)于 两点,若
两点,若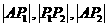 成等比数列,求
成等比数列,求 的值.
的值.
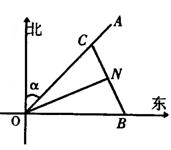 21. (本小题满分12分) 如图,一载着重危病人的火车从O地出发,沿射线OA行驶,其中
21. (本小题满分12分) 如图,一载着重危病人的火车从O地出发,沿射线OA行驶,其中 在距离O地
在距离O地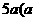 为正数)公里北偏
为正数)公里北偏
东β角的N处住有一位医学专家,其中sinβ= 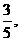
现有110指挥部紧急征调离O地正东p公里的B处
的救护车赶往N处载上医学专家全速追赶乘有重危
病人的火车,并在C处相遇,经测算当两车行驶的路
线与OB围成的三角形OBC面积S最小时,抢救最及时.
(1)求S关于p的函数关系;
(2)当p为何值时,抢救最及时.
19.(本小题满分12分) 我们知道由于 所以
所以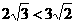 .已知
.已知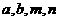 均为正数,且
均为正数,且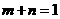 ,试比较
,试比较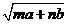 与
与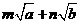 的大小.
的大小.
18.(本小题满分10分) 已知平面内点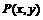 满足
满足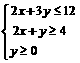 ,
,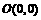 为坐标原点.请完成下列各问:
为坐标原点.请完成下列各问:
(I)若点Q的坐标为(1,1),求目标函数 的最大值和最小值.
的最大值和最小值.
(II)是否存在实数 ,使得有无穷多个P点,使得目标函数
,使得有无穷多个P点,使得目标函数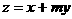 取得最小值,若存在,试求出
取得最小值,若存在,试求出 的值,若不存在请说明理由.
的值,若不存在请说明理由.
17.(本小题满分10分) 解关于x的不等式: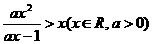
16.已知命题 ,
,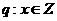 .若“p且q”与“非q”同时为假命题,则满足条件的
.若“p且q”与“非q”同时为假命题,则满足条件的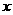 的集合为
的集合为
15.在平面几何中有如下特性:从角的顶点出发的一条射线上任意一点到角两边的距离之比为定值.类比上述性质,请叙述在立体几何中相应的特性为:
14.不等式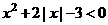 的解集是_____________________
的解集是_____________________
13.若关于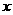 的不等式
的不等式 对任意
对任意 恒成立,则实数
恒成立,则实数 的取值范围是 .
的取值范围是 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com