
题目列表(包括答案和解析)
2.不注意各种不等式成立的条件,误用公式,特别是非负性的考虑.
[基础演练]
1.在运用均值不等式时,对等号成立的条件不注意往往出错;
2.在解答题中常与最值问题结合在一起以及函数的值域等知识一起考查,试题解法突出常规方法,淡化特殊技巧,一般以求最值的形式来问如练习题9.
[典例精析]
例1:(2005•全国1)当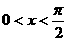 时,函数
时,函数 的最小值为( )
的最小值为( )
A.2 B. C.4 D.
C.4 D.
解析:
 ,当且仅当
,当且仅当 ,即
,即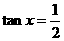 时,取“
时,取“ ”,∵
”,∵ ,∴存在
,∴存在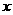 使
使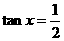 ,这时
,这时 ,
,
答案:C.
例2:(2005•福建) 下列结论正确的是( )
A.当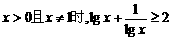 B.
B.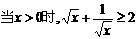
C. 的最小值为2 D.当
的最小值为2 D.当 无最大值
无最大值
解析:A中lgx不满足大于零,C中的最小值为2的x值取不到,D  当x=2时有最大值
当x=2时有最大值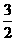 ,选B.
,选B.
答案:B
例3:(2005•重庆)若
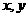 是正数,则
是正数,则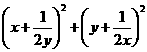 的最小值是( )
的最小值是( )
A.3
B.
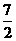 C.4
D.
C.4
D.

解析: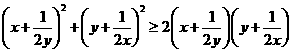
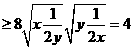
当且仅当
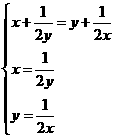 得
得 时.
时.
答案:C
[常见误区]
1.以二元均值不等式的考查最为常见,命题形式往往在选择题或填空题中,如例1,例2,例3.
1.掌握两个(不扩展到三个)正数的算术平均数不小于它们的几何平均数的定理,并会简单的应用.
1.2 算术平均数与几何平均数
[考点透视]
9.定义在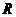 上的函数
上的函数 满足: 如果对任意x1, x2∈R,
满足: 如果对任意x1, x2∈R, 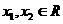 都有
都有
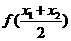 ≤
≤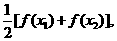
则称函数
 是
是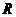 上的凹函数.
上的凹函数.
已知二次函数
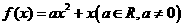 求证: 当
求证: 当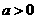 时, 函数
时, 函数 是凹函数.
是凹函数.
8.已知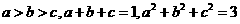 , 求证
, 求证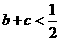 .
.
7.比较大小: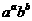 与
与 (
( 且
且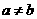 ).
).
6.若不等式 有且只有一个解,则实数
有且只有一个解,则实数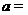 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com