
题目列表(包括答案和解析)
3.已知 则一定有 ( )
则一定有 ( )
A. B.
B.
C. D.
D.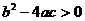
2.若x>0,y>0,且 恒成立,则a的最小值是 ( )
恒成立,则a的最小值是 ( )
A.2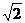 B.
B.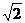 C.2 D.1
C.2 D.1
1.若a>b>1,P= ,Q=
,Q= (lga+lgb),R=lg(
(lga+lgb),R=lg( ),则 ( )
),则 ( )
A.R<P<Q B.P<Q<R C.Q<P<R D.P<R<Q
3.特别是在运用放缩法时可能会出现过大或过小的情形.
[基础演练]
2.例用均值不等式时不注意非负性导致错误;
1.不注意挖掘隐含条件从而导致错误;
2.考查不等式的基础知识、分类讨论的思想、综合思维能力,如例2,例3.
[典例精析]
例1:(2004•江苏)已知函数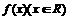 满足下列条件:对任意的实数x1,x2都有
满足下列条件:对任意的实数x1,x2都有
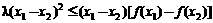
和 ,其中
,其中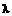 是大于0的常数.设实数a0,a,b满足
是大于0的常数.设实数a0,a,b满足  和
和 .
.
(1)证明: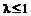 ,并且不存在
,并且不存在 ,使得
,使得 ;
;
(2)证明: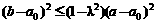 ;
;
(3)证明: .
.
解析:(1)任取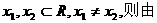
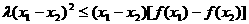
和 ②
②
可知
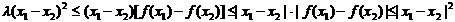 ,
,
从而
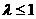 . 假设有
. 假设有 ①式知
①式知
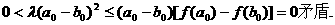
∴不存在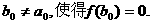
(2)由 ③
③
可知
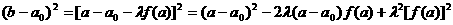 ④
④
由 ①式,得
①式,得 ⑤
⑤
由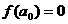 和②式知,
和②式知, ⑥
⑥
由⑤、⑥代入④式,得 
 .
.
(3)由③式可知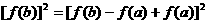

 (用②式)
(用②式)
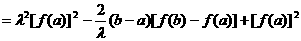
 (用①式)
(用①式)
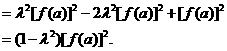
例2:(2003•北京) 设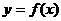 是定义在区间
是定义在区间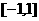 上的函数,且满足条件:
上的函数,且满足条件:
①
②对任意的
(1)证明:对任意的
(2)证明:对任意的
(3)在区间[-1,1]上是否存在满足题设条件的奇函数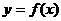 ,且使得
,且使得
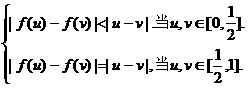
若存在,请举一例:若不存在,请说明理由.
解析:(1)由题设条件可知,当 时,有
时,有
即
(2)对任意的
当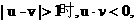 不妨设
不妨设 则
则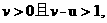
所以,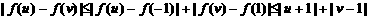
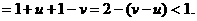
综上可知,对任意的 都有
都有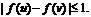
由(1)可得,当 时,
时,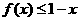
当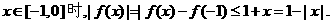
所以,当 因此,对任意的
因此,对任意的
当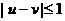 时,
时,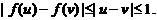 当
当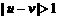 时,有
时,有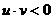
且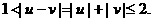
所以
综上可知,对任意的 都有
都有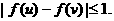
(3)满足所述条件的函数不存在.
理由如下,假设存在函数 满足条件,则由
满足条件,则由
得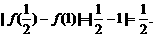 又
又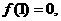 所以
所以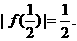 ①
①
又因为 为奇数,所以
为奇数,所以 由条件
由条件
得
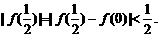 ② ①与②矛盾,所以假设不成立,即这样的函数不存在.
② ①与②矛盾,所以假设不成立,即这样的函数不存在.
例3:正项数列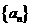 满足
满足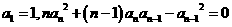
 .
.
(1)求 及
及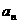 ;
;
(2) 试确定一个正整数N, 使当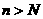 时, 不等式
时, 不等式
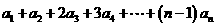 >
> 成立;
成立;
(3)求证: (1+ )
)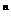 <
<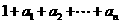 .
.
解析:(1)
 (
( -1)(
-1)(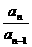 +1)=0,
+1)=0,
又∵ ,故
,故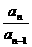 =
= ,
,  ,
,
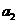 =
= =
=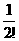 ,
,  =
=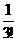 ,
, 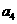 =
=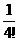 , …,
, …, 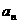 =
=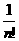 .
.
(2) 由 =
= =
=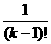 -
- (
( ),
),
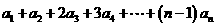
=1+( -
-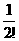 )+(
)+(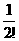 -
-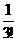 )+ … +(
)+ … +( -
-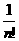 )=2-
)=2-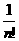
从而有2-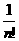 >
> , ∴
, ∴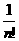 <
< , 即n!>121.
, 即n!>121.
∵5!=120, 6!=720, ∴n>5取N=5, n>N时, 原不等式成立.
(3) (1+ )
)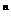 展开式通项:
展开式通项:
T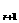 =C
=C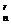 ·(
·( )
)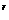 =
= ·
· ·
· · … ·
· … · ·
·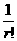 <
<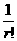 (r=0, 1, 2, 3, …, n)
(r=0, 1, 2, 3, …, n)
(1+ )
)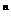 <
< +
+ +
+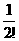 +
+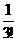 + … +
+ … +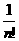 =
= 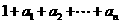 .
.
[常见误区]
1.不等式的证明的考查主要是与数列、函数、导数、向量等知识相结合考察不等式的证明方法特别是数学归纳法、综合法、比较法等方法的掌握,如例1.
2.理解不等式│a│-│b│≤│a+b│≤│a│+│b│
1.掌握分析法、综合法、比较法证明简单的不等式;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com