4. 在5件产品中,有3件一等品和2件二等品,从中任取2件,那么以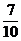为概率的事件是()

A.都不是一等品　　　 B.恰有一件一等品　

C.至少有一件一等品　 D.至多一件一等品

3.一个正方体的体积是8,则这个正方体的内切球的表面积是(　 )

A.　 B.　　 C.　 D.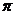

2.在北纬45°的纬度圈上有甲、乙两地,两地经度差为90°,则甲、乙两地最短距离为(设地球的半径为R)(　 )

A.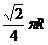　　　　 B.　 C.　 D.

1. 三个不重合的平面可把空间分成n部分,则n的所有可能取值为(　 )

A.4　　　　　　　 B. 4或6　 　　　 C.4或6或8　　　　　 D. 4或6或7或8

22．(本小题12分)

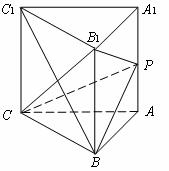
如图，直三棱柱ABC－A₁B₁C₁中，AA₁=BC，AB=AC， 且∠BAC=90°，P为AA₁的中点．

(Ⅰ)证明：BC₁⊥平面PB₁C；

(Ⅱ)求二面角B₁－PC－B的大小．

平顶山市2008-2009学年第二学期期末调研考试

21．(本小题12分)

甲、乙二人进行一次围棋比赛，约定先胜3局者获得这次比赛的胜利，比赛结束．假设在一局中，甲获胜的概率为0.6，乙获胜的概率为0.4，各局比赛结果相互独立．已知前2局中，甲、乙各胜1局．　 　　　

(Ⅰ)求再赛2局结束这次比赛的概率；

(Ⅱ)求甲获得这次比赛胜利的概率．

20．(本小题满分12分) 　 　　　

一个不透明的口袋内装有材质、重量、大小相同的7个小球，且每个小球的球面上要么只写有数字“08”，要么只写有文字“奥运”．假定每个小球每一次被取出的机会都相同，又知从中摸出2个球都写着“奥运”的概率是．现甲、乙两个小朋友做游戏，方法是：不放回从口袋中轮流摸取一个球，甲先取、乙后取，直到两个小朋友中有1人取得写着文字“奥运”的球时游戏终止．

(Ⅰ)求该口袋内装有写着数字“08”的球的个数；　 　　　

(Ⅱ)求当游戏终止时总取球次数不多于3的概率．

19．(本小题满分12分)

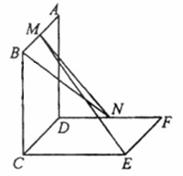
如图，已知两个正方形ABCD和DCEF不在同一平面内， M，N分别为AB，DF的中点．

(Ⅰ)用反证法证明：直线ME与BN是两条异面直线；

(Ⅱ)若平面ABCD⊥平面DCEF，求异面直线ME与BN所成的角的余弦值．

18．(本小题满分12分)

为支援西部开发，需要从8名男干部2名女干部中任选4人到西部某地任职，如果男性干部不少于3人，则称干部配置合理．　 　　　

(Ⅰ)求干部配置合理的概率；

(Ⅱ)若一年中对这些支援西部的干部配置三次，求其中恰有两次配置不合理的概率．

17．(本小题10分)

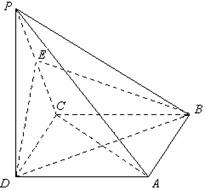
如图，在四棱锥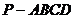中，底面ABCD是正方形， 侧棱底面ABCD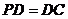，，E是PC的中点．

(Ⅰ)证明：PA∥平面EBD；

(Ⅱ)求EB与底面ABCD所成的角的正切值．