2．已知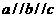直线，则直线至多可以确定平面的个数为　　　　　　　 (　　 )

A．1　 　　　　　　 B．2　　　　　　　　　　　　　　 C．3　　　 　　　　 D．4

答案：选C.　 理由：两平行直线可以确定一个平面，当三条平行直线不共面时可以确定三个平面.

只有一项是符合题目要求的．

1．已知，则的值是　　　　　　　　　　　　　　　　　 (　　 )

A．60　　　　 　　　　 B．50　　　　　　　　　　　　 C．45　　 　　　　 D．30

答案：选B.　 理由：由排列数公式知.

21.(本小题满分14分)

一种计算装置，有一数据入口A和一个运算出口B，按照下列运算程序操作：

①当从A 口输入自然数1时，从B出口得到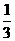，记为；

②当从A 口输入自然数n(n≥2)时，在B出口得到的结果f(n)是前一个结果f(n－1)的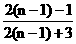倍.

(1) 当从A 口分别输入自然数2，3，4时，从B出口分别得到什么数？　 　　　

(2)试猜想f(n)的关系式，并证明你的结论；

(3)记S_n为数列{ f(n)}的前n项的和，当从B出口得到16144323的倒数时，求此时对应的S_n的值.

2009年南山区高二期末考试

20.(本小题满分14分)

某校举行环保知识大奖赛，比赛分初赛和决赛两部分，初赛采用选手选一题答一题的方式进行，每位选手最多有5次选题答题的机会，选手累计答对3题或答错3题即终止其初赛的比赛，答对3题者直接进入决赛，答错3题者则被淘汰，已知选手甲回答每个问题的正确率相同，并且答题相互之间没有影响，且连续两次答错的概率为.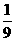 　 　　　

(1)求选手甲回答一个问题的正确率；　　　 (2)求选手甲进入决赛的概率；

(3)设选手甲在初赛中答题的个数为ξ，试写出ξ的分布列，并求ξ的数学期望.

19.(本小题满分14分)

某农科所对冬季昼夜温差与某反季节大豆种子发芽多少之间的关系进

行分析研究，他们记录了12月1日至5日的昼夜温差与每天100颗种子的发芽数，数据如下：

该农科所确定的研究方案是：先从五组数据中选取两组，用剩下的3

组数据求线性回归方程，再用被选取得两组数据进行检验.

(1) 求先选取两组数据恰好是不相邻两天数据的概率；

(2) 若先选取的是12月1日至5日的数据，请根据2日至4日的三组数据，求y关于x的线性回归方程；　 　　　

(3)若由回归方程得到的估计数据与检验数据的误差均不超过2颗，则认为得到的线性回归方程是可靠的，试判断(2)中所得的线性回归方程是否可靠？

18.(本小题满分14分)

如图，在几何体ABCDE中，DA⊥平面EAB，CB∥DA，EA⊥AB，

M是EC的中点，EA=DA=AB=2CB.请建立适当的空间直角坐标系，用空间向量知识解决下列问题.

(1)求证：DM⊥EB；　　 　 　　　

(2)求异面直线AB与CE所成角的余弦值；

(3)求二面角M-BD-A的余弦值.

17.(本小题满分12分)

某地区下岗人员免费提供财会和计算机培训，每名下岗人员可以选择参加一项培训、两项培训或不参加培训.已知参加财会培训的有60%，参加计算机培训的有75%，假设每个人对培训项目的选择均是相互独立的，且各人的选择相互之间没有影响.　

(1)任选1名下岗人员，求该人参加过培训的概率；　 　　　

(2)任选3名下岗人员，求这3人中至少有2人参加过培训的概率.

16.(本小题满分12分，最后结果用数字作答)

用0、1、2、3、4五个数字组成无重复数字的四位数. 　 　　　

(1)这样的四位数共有多少个？　　 　　

(2)若将这样的四位数按从小到大排列，则3204 是第几个数？

15.(几何证明选讲选做题)如图，PA、PB是是⊙O的切线，A、B为切点，

点C为⊙O上与A、B不重合的另一点，若∠ACB=120⁰， 则∠APB=　　 ．

14.(不等式选讲选做题) 已知x，y∈R*，且x+4y=1，则xy的最大值为__________.