4．α，β是两个不同的平面，m、n是平面α及β之外的两条不同直线．给出四个论断：①m⊥n　 ②α⊥β　 ③n⊥β　 ④m⊥α ．

以其中三个论断作为条件，余下一个论断作为结论，写出你认为正确的一个命题：　　　　　　　　　 ．

3．已知球O的半径是1，A、、C三点都在球面上，A、B两点和A、C两点的球面距离都是，B、C两点的球面距离是，则二面角B－OA－C的大小是(　 )

(A) 　　　　　(B)　　　　　 (C) 　　　　　(D)

2．在正三棱柱ABC-A₁B₁C₁中，若AB＝BB₁，则AB₁与C₁B所成的角的大小为　　　　　　　 　　　　　　　　　　　(　　 )

(A)60°　 (B)90°　 (C)105°　　 　 (D)75°

例1正六棱柱ABCDEF-A₁B₁C₁D₁E₁F₁的底面边长为1，侧棱长为，则这个棱柱的侧面对角线E₁D与BC₁所成的角是　　　　　　　　　　　 　　　　(　　 )

(A)90°　 　　　　　　 　(B)60°　 　　　　　　　　　 (C )45°　　　 　(D)30°

　例2 　是从点出发的三条射线，每两条射线的夹角均为，那么直线与平面所成角的余弦值是　　　　　　　　　　　　　　　 ( 　　)

(A)　　　 (B)　　　　 (C)　　　 　(D)

例3如图，∠BAD＝90°的等腰直角三角形ABD与正三角形CBD所在平面互相垂直，E是BC的中点，则AE与平面BCD所成角的大小为_____________．

例4若正三棱锥底面边长为4，体积为1，则侧面和底面所成二面角的大小等于　　 ____　 (结果用反三角函数值表示)．

例5在三棱锥S-ABC中，∠SAB=∠SAC=∠ACB=90°，AC=2，BC=，SB=．

(Ⅰ)证明：SC⊥BC；

(Ⅱ)求侧面SBC与底面ABC所成二面角的大小；

(Ⅲ)求异面直线SC与AB所成的角的大小(用反三角函数表示)．

例6已知如图斜三棱柱ABC-A₁B₁C₁的侧面A₁ACC₁与底面ABC垂直，∠ABC＝90°，BC＝2，AC＝2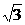，且AA₁⊥A₁C，AA₁＝A₁C．

(Ⅰ)求侧棱A₁A与底面ABC所成角的大小；

(Ⅱ)求侧面A₁ABB₁与底面ABC所成二面角的大小；

(Ⅲ)求侧棱B₁B和侧面A₁ACC₁的距离．

过关练习

1．正四棱锥的侧棱长与底面边长都是1，则侧棱与底面所成的角为　 (　 )

(A)75°　　 (B)60°　 (C)45°　 (D)30°

4． 已知正四棱锥的体积为12，底面的对角线长为，则侧面与底面所成的二面角等于　　　　　 ．

3． 已知正三棱柱ABC－A₁B₁C₁的所有棱长都相等,则与平面所成角的余弦值为　　　　　 ．

2． A₁B₁C₁-ABC是直三棱柱，∠BCA=90°，点D₁、F₁分别是A₁B₁、A₁C₁的中点，若BC=CA=CC₁，则BD₁与AF₁所成角的余弦值是(　　 )

(A)　 　　　　 　　(B)　　　　　 (C) 　　　　　　　　　 (D)

1．正六棱柱ABCDEF-A₁B₁C₁D₁E₁F₁的底面边长为1，侧棱长为，则这个棱柱的侧面对角线E₁D与BC₁所成的角是(　　 )

(A)90° 　　　　　　　　 　　(B)60°　 　　　　　　　 　(C)45°　 　　　　　 　　(D)30°

重点：①求异面直线所成的角；②求直线与平面所成的角；③求二面角．

难点：二面角的作法与求法．

空间角的计算在高考中通常有一道解答题，题目为中等难度，这是作为立体几何中重点考查的内容之一，解题时要注意计算与证明相结合．