5．明确均值不等式及其成立条件，会灵活应用均值不等式证明或求解最值。

4．会作二元一次不等式(组)表示的平面区域，会解简单的线性规划问题；

3．会解一元二次不等式，熟悉一元二次不等式、一元二次方程和二次函数的关系；

2．熟悉不等式的性质，能应用不等式的性质求解“范围问题”，会用作差法比较大小；

1．会用不等式(组)表示不等关系；

　⒐某商品进货价每件50元，据市场调查，当销售价格每件x元(50<x≤80)，每天销售的件数为P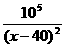＝，若想每天获得的利润最多，则销售价为多少元？．

　⒑如图所示，动物园要围成相同面积的长方形虎笼四间，一面可以利用原有的墙，其他各面用钢筋网围成。⑴现有可围36m长钢筋网材料，每间虎笼的长、宽各设计为多少时，可使每间虎笼面积最大？⑵若使每间虎笼面积为24m²，则每间虎笼的长、宽各设计为多少时，可始围成四间虎笼的钢筋网总长最小？

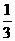　⒍光线透过一块玻璃，其强度要减弱，要使光线的强度减弱到原来的以下，至少需要这样的玻璃板__________块(lg2=0.3010,lg3=0.4771)．

　⒎Rt△ABC斜边长c=1，那么它的内切圆半径r的最大值为___________．

　⒏已知ab=1000，a>1，b<1，则的最大值是____________．

　⒈某产品今后四年的市场需求量依次构成数列{a_n}，n=1，2，3，4，并预测到年需求量第二年比第一年增长的百分率万P₁，第三年比第二年增长的百分率万P₂，第四年比第三年增长的百分率为P₃，且P₁+P₂+P₃＝1。给出以下数据⑴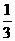，⑵，⑶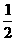，⑷，⑸，则其中可能成为这四年间市场需求量的年平均增长率的是(　　　)

　A．⑴⑵　　　B．⑴⑶　　C．⑵⑶⑷　　　D．⑵⑸

　⒉用一张钢板制作一个容积为4m³的无盖长方体水箱，可以用的长方形钢板有四种不同的规格(长×宽的尺寸如各选项所示，单位均为m)。若既要够用，分割的块数不超过5，又要所剩最少，则应选择的钢板的规格是(　　　)

　A．2×5　　B．2×5.5　　C．2×6.1　D．3×5

　⒊某工厂2006年生产利润逐月增加，且每月增加的利润相同，但由于厂家正在改造建设，一月份投入建设资金恰好与一月份利润相等，随着投入资金的逐月增加且每月增加的百分比相同，到12月投入资金又恰好与12月生产利润相同，问全年总利润W与全年总投入N的大小关系是(　　　)

　A．W>N　　B．W<N　　C．W=N　　 D．不能确定

　⒋生物学指出，生态系统中，在输入一个营养级的能量中，大约10%-20%的能量转入到下一个营养级，在H₁→H₂→H₃→H₄→H₅→H₆这条生物链中，若能使H₆获得10kj的热量，则需要H₁最多可提供的能量是(　　　)

　A．10⁴kj　　B．10⁵kj　　　　 C．10⁶kj　　　　　 D．10⁷kj

　⒌某商场对顾客实行购物优惠，规定一次购物付款总额：⑴如果不超过200元，则不予优惠；⑵如果超过200元但不超过500元，则按标价给予9折优惠；⑶如果超过500元，500元按⑵条给予优惠，超过500元的部分给予7折优惠。某人两次去购物，分别付款168元和423元，假设他只去一次购买上述同样的商品，则应付款是(　　　)元。

　A．413.7　　　B．513.7　　　C．546.6　　　D．548.7

20．如图，PA⊥平面ABCD，四边形ABCD是正方形，PA=AD=2，M、N分别是AB、PC的中点．

　　 (1)求二面角P-CD-B的大小；

(2)求证：平面MND⊥平面PCD；

(3)求点P到平面MND的距离．

四川省绵阳市08-09学年高二下学期期末教学质量测试

19．在某农场棉花试验基地，抽样测得某品种棉花纤维的纤度(表示纤维粗细的一种量)共有100个数据，将这些数据分组如右表：

(1)请补全答卷上的频率分布表和频率分布直方图；

(2)估计纤度落在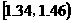中的概率及纤度不小于1.42的概率是多少？

(3)统计方法中，同一组数据常用该组区间的中点值(例如，的中点值是1.32)作为代表，据此，估计这块棉花试验基地的棉花纤维纤度的平均值(结果精确到0.01)．