
题目列表(包括答案和解析)
9.已知函数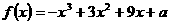 在区间
在区间 上的最大值为20,则它在该区间上的最小值为
( )
上的最大值为20,则它在该区间上的最小值为
( )
A. 13 B. 3 C. -3 D. -7
8.在一个袋子中装有标注数字1,2,3,4,5的五个小球,这些小球除标注的数字外完全相同.现在从中随机取出2个小球,在已知取出的小球标注的数字之和为偶数的情况下,则标注数字之和为4或6的概率是 ( )
A.  B.
B.
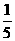 C.
C.
 D.
D.

7.已知数列 的前
的前 项和为
项和为 ,
, 且
且 ,利用归纳推理猜测
,利用归纳推理猜测 ( )
( )
A.  B.
B.
 C.
C.  D.
D.

6.如图, 、
、 、
、 表示三个开关,设在某段时间内
表示三个开关,设在某段时间内
他们正常工作的概率分别是0.9、0.8、0.7,那么该系统
正常工作的概率是( )
A. 0.994 B. 0.686 C. 0.504 D. 0.496
5.建立回归模型时,有下列步骤:
①得出结果后分析残差图是否有异常,若存在异常,则检查数据是否有误,或模型是否合适等;
②确定研究对象,明确哪个变量是解释变量,哪个变量是预报变量;
③按一定规则估计回归方程中的参数;
④由经验确定回归方程的类型;
⑤画出确定好的解释变量和预报变量的散点图,观察它们之间的关系.
则在下列操作顺序中正确的是 ( )
 A. ①②⑤③④ B. ②⑤④③① C. ②④③①⑤ D. ③②④⑤①
A. ①②⑤③④ B. ②⑤④③① C. ②④③①⑤ D. ③②④⑤①
4.函数 的导函数
的导函数 ( )
( )
A.  B.
B.  C.
C.  D.
D. 
3.甲、乙二人进行围棋比赛,采取“三局两胜制”,已知甲每局取胜的概率为 ,则甲获胜的概率为
( )
,则甲获胜的概率为
( )
A.  B.
B.

C.  D.
D.

2. 的展开式中,常数项为第( )项
的展开式中,常数项为第( )项
A. 3 B. 4 C. 5 D. 6
1.用数字0,1,2,3,4组成无重复数字的三位数的个数为 ( )
A. 24 B. 36 C. 48 D. 60
22.(本小题满分12分)如图, 为半圆直径,
为半圆直径, 为半圆圆心,且
为半圆圆心,且 ,
, 为线段
为线段 的中点,
的中点, ,曲线
,曲线 过点
过点 ,动点
,动点 在曲线
在曲线 上运动,且保持
上运动,且保持 的值不变.
的值不变.
(1)建立适当的平面直角坐标系,求曲线 的方程;
的方程;
 (2)若过点
(2)若过点 的直线
的直线 与曲线
与曲线 相交于不同的两点
相交于不同的两点 、
、 ,且点
,且点 ,设
,设 ,求
,求 的取值范围.
的取值范围.
解:(1)
以 所在直线分别为
所在直线分别为 轴、
轴、 轴,
轴, 为原点,建立平面直角坐标系,?
为原点,建立平面直角坐标系,?
∵ =2
=2
 .
.
∴曲线 为以原点为中心,
为以原点为中心, 、
、 为焦点的椭圆. 设其长半轴为a, 短半轴为b, 半焦距为c, 则
为焦点的椭圆. 设其长半轴为a, 短半轴为b, 半焦距为c, 则 , ∴
, ∴ ,
,  .
.
∴曲线 的方程为
的方程为 .
.
(2) 当直线l的斜率存在时,设直线l的方程为 ,
, ,
,

代入 , 得
, 得 .
.
由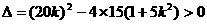 ,
得
,
得 .
.
由韦达定理得
由 得
得 ,代入上式得
,代入上式得
两式相除得 .
.
 ,
,
 ,
,


 ,∴
,∴ .
.
当 不存在时,显然
不存在时,显然
 (此时直线l与y轴重合).
(此时直线l与y轴重合).
综上所述, 的取值范围是
的取值范围是 .
.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com