
题目列表(包括答案和解析)
1.已知全集 ,集合
,集合 ,则( )
,则( )
A  B
B  C
C 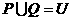 D
D 
22.(10分) (1)选修4-1:几何证明选讲
(1)选修4-1:几何证明选讲
证明:连接 (1分)
(1分)
在四边形 中,
中, ,
, ,
,


 、
、 、
、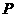 、
、 四点共圆.(5分)
四点共圆.(5分)
 .(6分)
.(6分)
又 ,
, ,而
,而


 、
、 、
、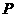 、
、 四点共圆.(10分)
四点共圆.(10分)
(2)选修4-4:坐标系与参数方程
解:设 ,(2分)
,(2分)
则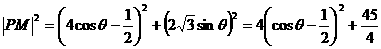 (6分)
(6分)
当 时,
时, ,此时
,此时 .(10分)
.(10分)
(3)选修4-5:不等式选讲
解:易知 或
或 所以
所以 (4分)
(4分)
要满足 对于一切非零实数
对于一切非零实数 均成立,只需满足
均成立,只需满足 ,(6分)
,(6分)
化简得 ,解得
,解得 ,
,
所以实数 的取值范围是
的取值范围是 (10分)
(10分)

21.(12分)解(1) 依题意
依题意 2分
2分
又∵ ,依题意
,依题意 ……………3分
……………3分

 ……………………………………4分
……………………………………4分
(2)由(1)可知,原方程为
设 …………………5分
…………………5分
令
令 ………………………………………7分
………………………………………7分
由
 |
(0,1) |
1 |
(1,+∞) |
 |
- |
0 |
+ |
 |
递减 |
0 |
递增 |
即 在
在 处有一个最小值0,即当
处有一个最小值0,即当 时,
时, >0,
>0, 只有一个解.
只有一个解.
即当x>0时,方程 有唯一解. ………………………………………8分
有唯一解. ………………………………………8分
(3) 当
当 时,
时,
 为减函数,其最小值为1.
………………………………………9分
为减函数,其最小值为1.
………………………………………9分
令 恒成立…………10分
恒成立…………10分
∴函数 在
在 为增函数,其最大值为2b-1,…………………11分
为增函数,其最大值为2b-1,…………………11分
依题意 ,解得
,解得 为所求范围. …………………………………12分
为所求范围. …………………………………12分
20. (10分)
解:设方案一,方案二中奖的概率分别为 ,
, ,
,
从袋中任意摸出1个球,为红球的概率为 ………………………………………2分
………………………………………2分
记按方案一摸出红球的个数为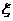 ,则
,则
 ………………………………………4分
………………………………………4分
 ………………………………………6分
………………………………………6分
因此 ………………………………………7分
………………………………………7分
又  ………………………………………9分
………………………………………9分
所以 ,方案一的中奖率更高一些. ………………………………………10分
,方案一的中奖率更高一些. ………………………………………10分
19.(10分)解:(1) ………………………2分
………………………2分
令 ,得
,得 或
或 ………………………………………3分
………………………………………3分
|
x |
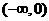 |
 |
 |
 |
 |
 |
- |
|
- |
|
+ |
 |
减函数 |
|
减函数 |
极小值 |
增函数 |
………………………………………5分
因此,函数 的单调递增区间为
的单调递增区间为 ,单调递减区间为
,单调递减区间为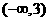 …………………6分
…………………6分
极小值为 ………………………………………7分
………………………………………7分
(2)由(1)得 的最小值为
的最小值为 ………………………………………8分
………………………………………8分
又 时,
时, ,
,
因此,要使方程 有两个实根,只需
有两个实根,只需 ……………………………………9分
……………………………………9分
解得 ………………………………………10分
………………………………………10分
18.(8分)解法一: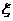 的所有可能值为0,1,2,3,4,(1分)
的所有可能值为0,1,2,3,4,(1分)
由等可能性事件的概率公式得

 (5分)
(5分)
从而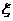 的分布列为 (6分)
的分布列为 (6分)
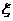 |
0 |
1 |
2 |
3 |
4 |
|
P |
 |
 |
 |
 |
 |
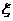 的期望为
的期望为 (8分)
(8分)
解法二:考察一位朋友是否在第三个景点下车为一次试验,这是4次独立重复试验.
 (5分)
(5分)
分布列与期望同上.(8分)
17.(6分)
解:设 ,则
,则 …………………………1分
…………………………1分
即
所以 ………………………………………3分
………………………………………3分
解得 ………………………………………4分
………………………………………4分
因此 ………………………………………6分
………………………………………6分
22.(本小题满分10分)请在下面三题中任选一题做答,如果多做,则按所做的第一题记分.
 (1)选修4-1:几何证明选讲
(1)选修4-1:几何证明选讲
如图, 是
是 的
的 边上的高,
边上的高, ,
, .
.
求证: 、
、 、
、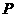 、
、 四点共圆.
四点共圆.
(2)选修4-4:坐标系与参数方程
在椭圆 上求一点
上求一点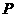 ,使点
,使点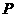 到点
到点 的距离
的距离 取最小值.
取最小值.
(3)选修4-5:不等式选讲
不等式 对于一切非零实数
对于一切非零实数 均成立,求实数
均成立,求实数 的取值范围.
的取值范围.
 东北师大附中
高二数学(理科)试卷
东北师大附中
高二数学(理科)试卷
命题人:暴偶奇 王晓晶 审题人:王艳平 2009-07-09
21.(本小题满分12分)已知函数 在
在 是增函数,
是增函数, 在
在 为减函数.
为减函数.
(1)求 ,
, 的表达式;
的表达式;
(2)求证:当 时,方程
时,方程 有唯一解;
有唯一解;
(3)当 时,若
时,若 在
在 内恒成立,求
内恒成立,求 的取值范围.
的取值范围.
20.(本小题满分10分)某班级在联欢会上设计了一个摸奖游戏,在一个口袋中装有3个红球和6个白球,这些球除颜色外完全相同,有两个备选的中奖方案:
方案一:从袋中任意摸出1个球,记下颜色后放回,连续摸三次,至少摸到2个红球视为中奖;
方案二:一次从袋中摸出3个球,至少摸到2个红球视为中奖.
你认为哪个方案的中奖率更高一些?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com