21.(本小题满分14分)

设向量在[0，1]上的最大值与最小值的和为a_n,又数列满足:

　 (1)求的表达式；

　 (2)求的表达式；　 　

　 (3)中，是否存在正整数k，使得对于任意的正整数n，都有成立？证明你的结论。

20．(本小题满分13分)

. 如图, 平行四边形中，，，,

平面，PA=2,点为中点,连结.

　 (1)若，，求证:平面平面；

(2)若，试探究在BC边上是否存在点Q,使得

，并说明理由.

19.(本小题满分12分)

设函数f(x)=x³+ax²－a²x－1，二次函数g(x)=ax²－x－1.

(1)若a<0，求f(x)的单调区间；

(2)当函数y= f(x)与y= g(x)的图象只有一个公共点且g(x)存在最大值时，记f(x)的最大值为h(a)，求函数h(x)的解析式；　 　

(3)若函数f(x)与g(x)在区间(a－2，a)内均为增函数，求实数a的取值范围(一、二、五中必做，其它学校选做).

18．(本小题满分12分)

已知以点P为圆心的圆过点A(－1,0)和B(3,4),线段AB的垂直平分线交圆P于点C、D,且|CD|=,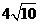 　 　

(1) 求直线CD的方程；

(2)求圆P的方程；

(3)设点Q在圆P上，试探究使△QAB的面积为8的点Q共有几个？证明你的结论(一、二、五中必做，其它学校选做).

17. (本小题满分12分)

已知直线l的方程为，从不同的直线l中任取一条。

　 (1)求所取直线的倾斜角大于的概率；　 　

　 (2)求所取直线在x轴上的截距与在y轴上截距之差小于7的概率。

16．(本小题满分12分)

在直角坐标系xoy中，角的顶点为坐标原点,始边在x轴的正半轴上.

(1)当角的终边为射线l：y=x (x≥0)时,求的值；

(2) 已知,试求的取值范围．　 　

15．给出下列五个命题：①不等式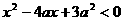的解集为；

②“”是“”的充分不必要条件；

③若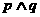为假命题，则p、q均为假命题；

④函数的图像与直线至多有一个交点；

⑤若角，β满足cos·cos＝1，则+)＝0.　

其中所有正确命题的序号是　　　　　　　　

14. 若不等式组表示的平面区域是一个三角形，则的取值范围是　　 　　　　　．　 　

13．某中学号召学生在暑假期间至少参加一次社会公益活动(以下简称活动)．该校文学社共有100名学生，他们参加活动的次数统计如图所示．则从文学社中任意选1名学生，他参加活动次数为3的概率是　　　　、该文学社学生参加活动的人均次数为　　．

12．为了测算如图阴影部分的面积，作一个变长为6的正方形将其

包含在内，并向正方形内随机投掷800个点，已知恰有200个点落

在阴影部分内，据此，可估计阴影部分的面积是____________.