
题目列表(包括答案和解析)
5.方差:
= (x12+x22+ x32+…+xn2-n
(x12+x22+ x32+…+xn2-n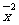 ).
).
用样本方差的大小估计总体数据波动性的好差(方差大波动差) .
4.平均数:(均值)  .
.
注:若取值为 的频率分别为
的频率分别为 ,则
,则
3.茎叶图:“茎”是指中间的一列数,“叶”就是从“茎”的旁边生长出来的数.
作用:表示样本数据的分布情况,
优点:①从统计图上没有信息的损失,所有的信息都可以从茎叶图中得到;
②茎叶图可以随时记录与表示.[茎叶图一般只能表示两位的整数]
2.总体分布的估计:用样本估计总体,是研究统计问题的一个基本思想方法.
(1)频率分布表:用样本的频率分布估计总体的概率分布.
注:样本频率分布表的作法:
①算数据极差 ,全距为
,全距为 ;
;
②决定组距和组数: ,一般分成10组左右;
,一般分成10组左右;
③决定分点,分点的数值取比样本中的数据多一位小数;
④列频率分布表;
(2)频率直方图
注:①频率直方图的纵轴(小矩形的高)是“ ”,横轴一般是数据的大小.
”,横轴一般是数据的大小.
频率=小矩形面积=组距× .
.
②各组频率之和等于1,即各小矩形面积之和等于1.
1.抽样方法:
(1)简单随机抽样(抽签法、随机数表法)适用于总体个数较少时,主要特征是从总体中逐个抽取.
(2)系统抽样:将总体平均分成几个部分,按照一定的规则,从每部分中抽取一个个体作为样本.
[抽取 个样本就将总体平均分成
个样本就将总体平均分成 部分,每部分中抽取一个个体,适用于总体中个体个数较多.]
部分,每部分中抽取一个个体,适用于总体中个体个数较多.]
方法:①每部分的间隔 ,若
,若 不是整数,在总体中剔除一些个体.
不是整数,在总体中剔除一些个体.
②将总体编号,确定起始编号 ,将编号为
,将编号为 ,
, ,
,
 的个体抽出.
的个体抽出.
(3)分层抽样:主要特征分层按比例抽样,适用于总体由差异明显的几部分组成.
注:共同点:每个个体被抽到的概率都相等( ).
).
6.已知两边和其中一边对角解斜三角形有两解或一解(见图示)





一解 两解 一解 一解
5.三角形形状的确定:
基本方法:化边为角或化角为边.
基本思路:寻求边与边之间的数量关系,或求出角的大小.常用用正弦定理进行代换,找出三角形的边、角关系,然后作出判断.
4.余弦定理 :  变形 :
变形 : 
(1)基本题型 :
①已知三边,解三角形:由余弦定理和内角和定理求角,在有解时只有一解.
②已知两边及夹角,解三角形:先由余弦定理求第三边,再由正弦定理与内角和定理求角,有一解.
(2)余弦定理是勾股定理的推广:判断 为锐角
为锐角 ,
,
 为直角
为直角 ,
, 为钝角
为钝角 .
.
3.三角形内角和定理 :
在△ABC中,


三角形中的基本关系:
①在△ABC 中: ;
;
② ,
,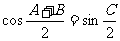 ;
; 
③在△ABC 中, ,… 在△ABC 中,
,… 在△ABC 中, ,…
,…
2. 三角形面积定理 :
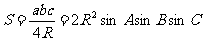
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com