例 1　 证明：若x²+y²＝0 , 则x＝y＝0 .

写出下列命题的逆命题、否命题及逆否命题，并分别判断它们的真假.

问题1：若f(x)是正弦函数，则f(x)是周期函数.

问题2：如果x＞10 , 那么x＞0 .

问题3：若b²－4ac＝0 , 则方程ax²+bx+c＝0 (a≠0)有两个相等的实根.

问题4：已知a,b∈R , 若a＝0 , 则ab＝0 .　

问题5：若x²－3x+2＝0 ，则x＝2 .

思考1？ 观察上面5个例子中的原命题、逆命题、否命题以及逆否命题，你能说出每个例子中任意两个命题之间的相互关系吗？

思考2？ 观察上面5个例子中的原命题、逆命题、否命题以及逆否命题，你能说出每个例子中的四种命题的真假性有几种情况吗？

结合上面的5个实例和思考2，你能从中发现四种命题的真假性间有什么规律吗？

知识导读，由于原命题和它的逆否命题有相同的真假性，所以我们在直接证明某一个命题为真命题有困难时，可以通过证明它的逆否命题为真命题，来间接地证明原命题为真命题。

4．若直线与圆锥曲线交于两点，则弦长为　 或；

(由方程 消去y得到，,为直线的斜率，).

3．以抛物线上的点为圆心，焦半径为半径的圆必与准线相切；

以抛物线焦点弦为直径的圆，必与准线相切；

以抛物线的焦半径为直径的圆必与过顶点垂直于轴的直线相切.

2．圆锥曲线的焦半径公式如下图：

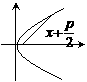
注：椭圆的焦半径公式和．

双曲线的焦半径公式

抛物线的焦半径公式

1．圆锥曲线的第二定义：一个动点P到定点F的距离与P到定直线的距离的比为.

若0＜＜1，则动点P的轨迹是椭圆；

若=1，则动点P的轨迹是抛物线；

若＞1，则动点P的轨迹是双曲线.

注：　 ()

　　 　“点点距为分子、点线距为分母” ()

12、已知曲线 y = x³ + x－2 在点 P₀ 处的切线 　平行直线4x－y－1=0，且点 P₀ 在第三象限,⑴求P₀的坐标; ⑵若直线 　, 且 l 也过切点P₀ ,求直线l的方程。

11、求垂直于直线并且与曲线相切的直线方程。

10、已知直线与曲线相切于点，则。

9、函数的导数为